题目内容
下列几个命题,正确的有
①方程x2+(a-3)x+a=0有一个正实根,一个负实根,则a<0;
②若幂函数y=xm2+2m-3的图象与坐标轴没有交点,则m的取值范围为(-3,1)
③若f(x+1)为偶函数,则有f(x+1)=f(-x-1);
④函数y=f(2x)的定义域为[1,2],则函数y=f(x)的定义域为[0,1].
①
①
.(填序号)①方程x2+(a-3)x+a=0有一个正实根,一个负实根,则a<0;
②若幂函数y=xm2+2m-3的图象与坐标轴没有交点,则m的取值范围为(-3,1)
③若f(x+1)为偶函数,则有f(x+1)=f(-x-1);
④函数y=f(2x)的定义域为[1,2],则函数y=f(x)的定义域为[0,1].
分析:根据韦达定理及一元二次方程根的个数与△的关系,可以判断①的真假;根据幂函数的图象和性质,可以判断②的真假;根据函数的对称性及轴对称函数解析式与对称轴的关系,可以判断③的真假;根据复数函数定义域的求法,根据已知求出函数y=f(x)的定义域,即可得到答案.
解答:解:若方程x2+(a-3)x+a=0有一个正实根,一个负实根,则△>0,且x1•x2=a<0,解得a<0,故①正确;
若幂函数y=xm2+2m-3的图象与坐标轴没有交点,则m2+2m-3≤0,解得m的取值范围为[-3,1];
若f(x+1)为偶函数,则表示函数若f(x)的图象关于直线x=1对称,而f(x+1)=f(-x-1)表示f(x)的图象关于直线x=0(y轴)对称,故③错误;
若函数y=f(2x)的定义域为[1,2],则函数y=f(x)的定义域为[2,4],故④错误;
故答案为:①
若幂函数y=xm2+2m-3的图象与坐标轴没有交点,则m2+2m-3≤0,解得m的取值范围为[-3,1];
若f(x+1)为偶函数,则表示函数若f(x)的图象关于直线x=1对称,而f(x+1)=f(-x-1)表示f(x)的图象关于直线x=0(y轴)对称,故③错误;
若函数y=f(2x)的定义域为[1,2],则函数y=f(x)的定义域为[2,4],故④错误;
故答案为:①
点评:本题考查的知识点是函数的定义域及其求法,函数奇偶性的性质,幂函数的性质,函数的零点与方程的根的关键,熟练掌握函数与方程之间的辩证关系,掌握初等基本函数的性质是解答此类问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
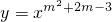 的图象与坐标轴没有交点,则m的取值范围为(-3,1)
的图象与坐标轴没有交点,则m的取值范围为(-3,1)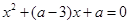 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则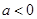 ;
;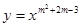 的图象与坐标轴没有交点,则m的取值范围为
的图象与坐标轴没有交点,则m的取值范围为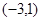
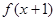 为偶函数,则有
为偶函数,则有 ;
;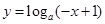 的图像可由函数
的图像可由函数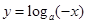 向右平移1个单位得到.
向右平移1个单位得到.