题目内容
已知四棱锥 ,侧面
,侧面 底面
底面 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面 为菱形,且
为菱形,且 .
.

(1)求证: ;
;
(2)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
(1)证明见解析;(2)2.
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等;(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)取 中点
中点 ,连结
,连结 .
.
侧面 为等边三角形,底面
为等边三角形,底面 为菱形且
为菱形且
 2分
2分
 4分
4分
 5分
5分
(2)侧面
 底面
底面 ,侧面
,侧面
 底面
底面 =
= ,
,
 ,
, 
 7分
7分

 9分
9分

所以四棱锥 的体积为2. 12分
的体积为2. 12分
考点:1、直线与直线垂直的判定;2、求几何体的体积.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 为异面直线,
为异面直线, 平面
平面 ,
, 平面
平面 ,
,

 ,则直线
,则直线
 对应的点位于
对应的点位于 的方程x2-2x+a+b=0无实数根的概率为 ( )
的方程x2-2x+a+b=0无实数根的概率为 ( ) B.
B. C.
C. D.
D.
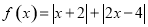 ,
,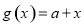 .
.
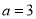 时,解不等式
时,解不等式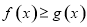 ;
; 的图象,根据图象求使
的图象,根据图象求使 恒成立的实数
恒成立的实数 的取值范围.
的取值范围. ,则
,则 .
. 的图象向右平移
的图象向右平移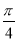 个单位后得到函数
个单位后得到函数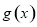 ,则
,则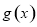 具有性质( )
具有性质( ) ,图象关于直线
,图象关于直线 对称
对称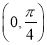 上单调递增,为奇函数
上单调递增,为奇函数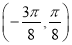 上单调递增,为偶函数
上单调递增,为偶函数 ,图象关于点
,图象关于点 对称
对称 ,则
,则 的展开式中常数项为 .
的展开式中常数项为 . 的公比为
的公比为 ,前
,前 项和为
项和为 .若
.若 ,则
,则 ,
, .
.