题目内容
已知函数f(x)=4x3+ax2+bx+15在x=-1与x= 处有极值.
处有极值.
(1)求出函数的单调区间;
(2)求f(x)在[-1,2]上的最值.
解:f′(x)=12x2+2ax+b,依题意有f′(-1)=0,f( )=0,
)=0,
即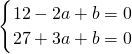 得
得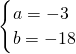
所以f′(x)=12x2-6x-18,
(1)f′(x)=12x2-6x-18<0,
∴(-1, )是函数的减区间
)是函数的减区间
(-∞,-1),( ,+∞)是函数的增区间.
,+∞)是函数的增区间.
(2)f(-1)=16,
f( )=-
)=-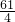 ,
,
f(2)=-11
∴最大值为16,最小值为-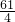 .
.
分析:首先求出函数的导数,然后f′(-1)=0,f′( )=0,解出a、b的值,进而求出导数.
)=0,解出a、b的值,进而求出导数.
(1)f′(x)<0,求出函数的单调区间;
(2)由(1)求出端点处函数值,从而求出函数f(x)在[-1,2]上的最大值和最小值.
点评:此题主要考查多项式函数的导数,函数单调性的判定,函数最值,函数、方程等基础知识,考查运算求解能力、推理论证能力及分析与解决问题的能力,难度不大.
 )=0,
)=0,即
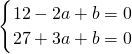 得
得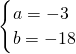
所以f′(x)=12x2-6x-18,
(1)f′(x)=12x2-6x-18<0,
∴(-1,
 )是函数的减区间
)是函数的减区间(-∞,-1),(
 ,+∞)是函数的增区间.
,+∞)是函数的增区间.(2)f(-1)=16,
f(
 )=-
)=-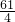 ,
,f(2)=-11
∴最大值为16,最小值为-
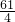 .
.分析:首先求出函数的导数,然后f′(-1)=0,f′(
 )=0,解出a、b的值,进而求出导数.
)=0,解出a、b的值,进而求出导数.(1)f′(x)<0,求出函数的单调区间;
(2)由(1)求出端点处函数值,从而求出函数f(x)在[-1,2]上的最大值和最小值.
点评:此题主要考查多项式函数的导数,函数单调性的判定,函数最值,函数、方程等基础知识,考查运算求解能力、推理论证能力及分析与解决问题的能力,难度不大.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目