题目内容
已知函数f(x)=a•2x+b的图象经过A(1,1),B(2,3)及C(n,Sn),其中Sn为数列{an}的前n项和,n∈N*.
(Ⅰ)求{an}的通项公式及前n项和Sn;
(Ⅱ)若{cn}中,cn=n(6an-1),求数列{cn}的前n项和Tn;
(Ⅲ)试比较(Ⅱ)中的Tn与 的大小并说明理由.
的大小并说明理由.
(本小题14分)
解:(Ⅰ)由f(x)=a•2x+b的图象经过A(1,1),B(2,3)两点 ,
,
∴f(x)=2x-1,
又C(n,Sn)在f(x)的图象上 ,
,
当n=1时,a1=S1=1;
当n≥2时, ,
,
∴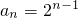 .
.
(Ⅱ)由(Ⅰ)知,

 ,
,
令 ,
,
由错位相减法可求得 ,
,
又 ,
,
故 .
.
(Ⅲ)由
当n=1时,6(n-1)[2n-(2n+1)]=0,
当n=2时,6(n-1)[2n-(2n+1)]=-6,
当n=3时,6(n-1)[2n-(2n+1)]=12,
下证n≥3时, ,
,
即证n≥3时,2n>2n+1,
∵n≥3时, 成立,
成立,
∴n≥3时, 成立,
成立,
综上所述:n=1时, ;
;
n=2时, ;
;
n≥3时, .
.
分析:(Ⅰ)由f(x)=a•2x+b的图象经过A(1,1),B(2,3)两点 ,故f(x)=2x-1,又C(n,Sn)在f(x)的图象上
,故f(x)=2x-1,又C(n,Sn)在f(x)的图象上 ,由此能求出{an}的通项公式及前n项和Sn.
,由此能求出{an}的通项公式及前n项和Sn.
(Ⅱ)由(Ⅰ)知,
 ,令
,令 ,由错位相减法可求得
,由错位相减法可求得 ,由此能求出数列{cn}的前n项和Tn.
,由此能求出数列{cn}的前n项和Tn.
(Ⅲ)由 ,能比较Tn与
,能比较Tn与 的大小并说明理由.
的大小并说明理由.
点评:本题考查数列与函数的综合,考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
解:(Ⅰ)由f(x)=a•2x+b的图象经过A(1,1),B(2,3)两点
 ,
,∴f(x)=2x-1,
又C(n,Sn)在f(x)的图象上
 ,
,当n=1时,a1=S1=1;
当n≥2时,
 ,
,∴
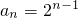 .
.(Ⅱ)由(Ⅰ)知,

 ,
,令
 ,
,由错位相减法可求得
 ,
,又
 ,
,故
 .
.(Ⅲ)由

当n=1时,6(n-1)[2n-(2n+1)]=0,

当n=2时,6(n-1)[2n-(2n+1)]=-6,

当n=3时,6(n-1)[2n-(2n+1)]=12,

下证n≥3时,
 ,
,即证n≥3时,2n>2n+1,
∵n≥3时,
 成立,
成立,∴n≥3时,
 成立,
成立,综上所述:n=1时,
 ;
;n=2时,
 ;
;n≥3时,
 .
.分析:(Ⅰ)由f(x)=a•2x+b的图象经过A(1,1),B(2,3)两点
 ,故f(x)=2x-1,又C(n,Sn)在f(x)的图象上
,故f(x)=2x-1,又C(n,Sn)在f(x)的图象上 ,由此能求出{an}的通项公式及前n项和Sn.
,由此能求出{an}的通项公式及前n项和Sn.(Ⅱ)由(Ⅰ)知,

 ,令
,令 ,由错位相减法可求得
,由错位相减法可求得 ,由此能求出数列{cn}的前n项和Tn.
,由此能求出数列{cn}的前n项和Tn.(Ⅲ)由
 ,能比较Tn与
,能比较Tn与 的大小并说明理由.
的大小并说明理由.点评:本题考查数列与函数的综合,考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目