题目内容
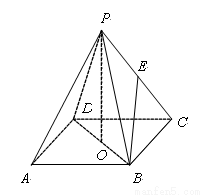
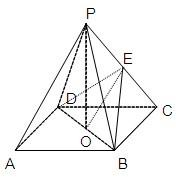 如图ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(1)PA∥平面BDE;
(2)平面PAC⊥平面BDE.
(3)若PO=1,AB=2,则异面直线OE与AD所成角的余弦值.
分析:(1)连接AC、OE,由中位线定理得PA∥EO,再由线面平行的判定定理得PA∥面BDE;
(2)由PO⊥底面ABCD,得PO⊥BD.再证得BD⊥平面由面面垂直的判定定理证得平面PAC⊥平面BDE;
(3)由(1)知,PA∥EO,知∠PAD为异面直线OE与AD所成角.
(2)由PO⊥底面ABCD,得PO⊥BD.再证得BD⊥平面由面面垂直的判定定理证得平面PAC⊥平面BDE;
(3)由(1)知,PA∥EO,知∠PAD为异面直线OE与AD所成角.
解答: 证明:(1)连接AC、OE,AC∩BD=O,
证明:(1)连接AC、OE,AC∩BD=O,
在△PAC中,∵E为PC中点,O为AC中点.∴PA∥EO,
又∵EO?平面EBD,PA?平面EBD,∴PA∥面BDE.
(2)∵PO⊥底面ABCD,∴PO⊥BD.
又∵BD⊥AC,∴BD⊥平面PAC.
又BD?平面BDE,∴平面PAC⊥平面BDE.
(3)由(1)知,PA∥EO,
∴∠PAD为异面直线OE与AD所成角.
∵O是正方形的中心,PO⊥底面ABCD
∴PD=
=
=
,
PA=
=
=
,
∴在△APD中,PA=PD,△APD是等腰三角形.
∴cos∠PAD=
=
=
.
 证明:(1)连接AC、OE,AC∩BD=O,
证明:(1)连接AC、OE,AC∩BD=O,在△PAC中,∵E为PC中点,O为AC中点.∴PA∥EO,
又∵EO?平面EBD,PA?平面EBD,∴PA∥面BDE.
(2)∵PO⊥底面ABCD,∴PO⊥BD.
又∵BD⊥AC,∴BD⊥平面PAC.
又BD?平面BDE,∴平面PAC⊥平面BDE.
(3)由(1)知,PA∥EO,
∴∠PAD为异面直线OE与AD所成角.
∵O是正方形的中心,PO⊥底面ABCD
∴PD=
| PO2+OD2 |
| 1+2 |
| 3 |
PA=
| PO2+OA2 |
| 1+2 |
| 3 |
∴在△APD中,PA=PD,△APD是等腰三角形.
∴cos∠PAD=
| ||
| PA |
| 1 | ||
|
| ||
| 3 |
点评:本题主要考查线面平行和线面垂直的判定定理,和异面直线所成的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
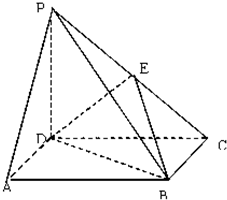 如图ABCD是正方形,PD⊥面ABCD,PD=DC,E是PC的中点.
如图ABCD是正方形,PD⊥面ABCD,PD=DC,E是PC的中点.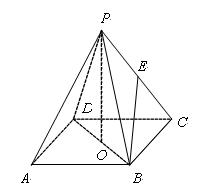
 底面ABCD,E是PC的
底面ABCD,E是PC的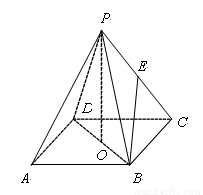
 底面ABCD,E是PC的
底面ABCD,E是PC的