题目内容
（本小题满分12分）
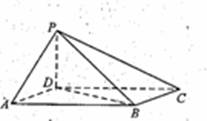如图，四棱锥
中，底面ABCD为平行四边形，
，
，
底面ABCD．
（I）证明：
；
（II）设PD=AD=1，求棱锥D-PBC的高．
解：
（Ⅰ）因为
， 由余弦定理得
从而BD2+AD2= AB2，故BD
AD
又PD底面ABCD，可得BDPD
所以BD平面PAD. 故 PABD
（Ⅱ）如图，作DEPB，垂足为E．已知PD底面ABCD，则PDBC．由（Ⅰ）知BDAD，又BC//AD，所以BCBD．
故BC平面PBD，BCDE．
则DE平面PBC．
由题设知，PD=1，则BD=
，PB=2，
根据BE·PB=PD·BD，得DE=
，
即棱锥D—PBC的高为
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
