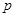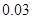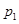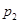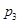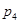题目内容
某同学在暑假的勤工俭学活动中,帮助某公司推销一中产品,每推销1件产品他可获利润4元,第1天推销了12件,之后他加强了宣传,从第2天起,每天比前一天多推销3件,问:
(1)该同学第6天所获利润是多少元?
(2)该同学参加这次活动的时间至少达到多少天,所获得的总利润才能不少于1020元.
(1)该同学第6天所获利润是多少元?
(2)该同学参加这次活动的时间至少达到多少天,所获得的总利润才能不少于1020元.
分析:(1)由题意,利润组成以48元为首项,12元为公差的等差数列,从而可求该同学第6天所获利润是多少元?
(2)利用等差数列的求和公式求和,再建立不等式,即可得出结论.
(2)利用等差数列的求和公式求和,再建立不等式,即可得出结论.
解答:解:(1)由题意,利润组成以48元为首项,12元为公差的等差数列,a6=48+(6-1)×12=108元;
(2)由题意,Sn=48n+
×12≥1020
∴n2+7n-170≥0
∴(n+10)(n-7)≥0
∵n≥1
∴n≥7
∴该同学参加这次活动的时间至少达到7天,所获得的总利润才能不少于1020元.
(2)由题意,Sn=48n+
| n(n-1) |
| 2 |
∴n2+7n-170≥0
∴(n+10)(n-7)≥0
∵n≥1
∴n≥7
∴该同学参加这次活动的时间至少达到7天,所获得的总利润才能不少于1020元.
点评:本题考查等差数列的通项与求和,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投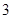 次:在
次:在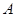 处每投进一球得
处每投进一球得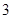 分,在
分,在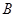 处每投进一球得
处每投进一球得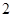 分;如果前两次得分之和超过
分;如果前两次得分之和超过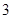 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在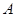 处的命中率
处的命中率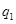 为
为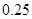 ,在
,在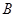 处的命中率为
处的命中率为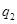 ,该同学选择先在
,该同学选择先在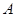 处投一球,以后都在
处投一球,以后都在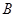 处投,用
处投,用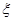 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
(1) 求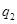 的值;
的值; (2)
求随机变量
(2)
求随机变量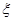 的数学期望
的数学期望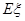 ;
;
(3) 试比较该同学选择都在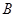 处投篮得分超过
处投篮得分超过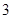 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过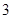 分的概率的大小.
分的概率的大小.
(本小题满分13分)在某校组织的一次篮球定点投篮训练中,规定每人最多投 次;在
次;在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在 处的命中率
处的命中率 为
为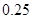 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
p |
0.03 |
P1 |
P2 |
P3 |
P4 |
(1)求 的值;
的值;
(2)求随机变量 的数学期望E
的数学期望E .
.
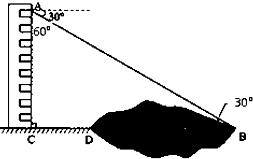 如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D处与C、B在同一条直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取
如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D处与C、B在同一条直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取