题目内容
已知:函数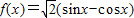 .
.(1)求函数f(x)的最小正周期和值域;
(2)若函数f(x)的图象过点
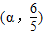 ,
,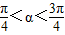 .求
.求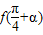 的值.
的值.
【答案】分析:(1)利用辅助角公式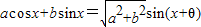 将函数
将函数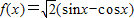 转化为
转化为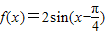 ,函数f(x)的最小正周期和值域可求;
,函数f(x)的最小正周期和值域可求;
(2)解法一:将(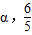 )代入
)代入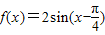 ,可得
,可得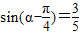 ,根据
,根据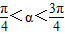 ,可求
,可求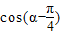 ,
,
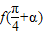 =2sinα=
=2sinα=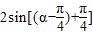 ,利用两角和的正弦公式可使问题得到解决;
,利用两角和的正弦公式可使问题得到解决;
解法二:将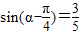 展开得
展开得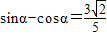 ,根据题中条件可得
,根据题中条件可得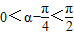 ,
,
从而得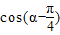 =
= ,展开得
,展开得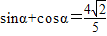 ,解关于sinα,cosα的方程组可求得sinα,
,解关于sinα,cosα的方程组可求得sinα,
又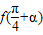 =2sinα,问题即可得到解决;
=2sinα,问题即可得到解决;
解法三:由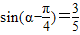 可求
可求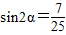 ,根据α的范围可求
,根据α的范围可求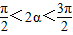 ,
,
利用sin22α+cos22=1求得 cos2α=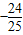 ,
,
由升幂公式可得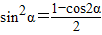 ;结合
;结合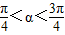 可求sinα,又
可求sinα,又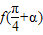 =2sinα,问题得到解决.
=2sinα,问题得到解决.
解答: 解:(1)
解:(1)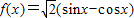 =
=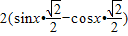 =
=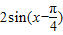 ---(3分)
---(3分)
∴函数的最小正周期为2π,值域为{y|-2≤y≤2}.
(2)解法1:依题意得: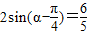 ,
,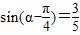 ,
,
∵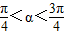 .∴
.∴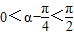 ,∴
,∴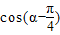 =
=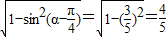
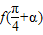 =
=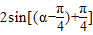
∵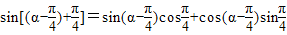 =
=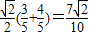
∴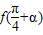 =
=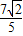
解法2:依题意得: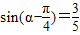 ,得
,得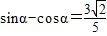 ----①
----①
∵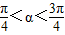 .∴
.∴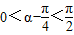 ,∴
,∴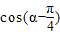 =
=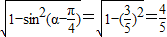
由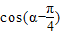 =
= 得
得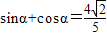 -----------②
-----------②
①+②得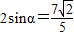 ,∴
,∴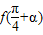 =
=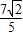
解法3:由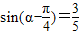 得
得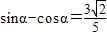 ,
,
两边平方得,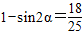 ,
,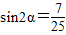 ,
,
∵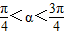 .∴
.∴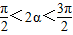 由
由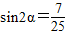 >0知
>0知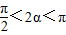
∴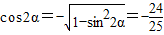 ,由cos2α=1-2sin2α,得
,由cos2α=1-2sin2α,得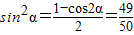
∴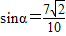 ∴
∴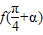 =
=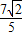 .
.
点评:本题考查正弦函数性质,解决的方法灵活,解法一侧重拼凑角的方法,考查两角和的正弦公式的应用,解法二侧重方程组思想方法,解法三侧重于倍角公式,升幂公式的考查,属于中档题.
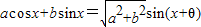 将函数
将函数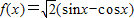 转化为
转化为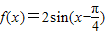 ,函数f(x)的最小正周期和值域可求;
,函数f(x)的最小正周期和值域可求;(2)解法一:将(
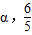 )代入
)代入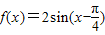 ,可得
,可得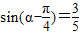 ,根据
,根据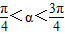 ,可求
,可求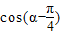 ,
,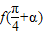 =2sinα=
=2sinα=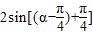 ,利用两角和的正弦公式可使问题得到解决;
,利用两角和的正弦公式可使问题得到解决;解法二:将
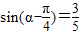 展开得
展开得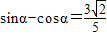 ,根据题中条件可得
,根据题中条件可得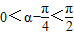 ,
,从而得
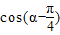 =
= ,展开得
,展开得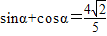 ,解关于sinα,cosα的方程组可求得sinα,
,解关于sinα,cosα的方程组可求得sinα,又
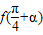 =2sinα,问题即可得到解决;
=2sinα,问题即可得到解决;解法三:由
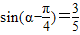 可求
可求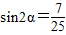 ,根据α的范围可求
,根据α的范围可求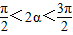 ,
,利用sin22α+cos22=1求得 cos2α=
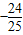 ,
,由升幂公式可得
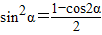 ;结合
;结合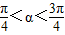 可求sinα,又
可求sinα,又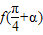 =2sinα,问题得到解决.
=2sinα,问题得到解决.解答:
 解:(1)
解:(1)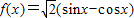 =
=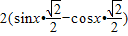 =
=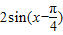 ---(3分)
---(3分)∴函数的最小正周期为2π,值域为{y|-2≤y≤2}.
(2)解法1:依题意得:
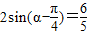 ,
,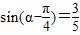 ,
,∵
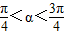 .∴
.∴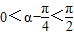 ,∴
,∴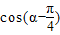 =
=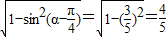
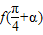 =
=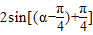
∵
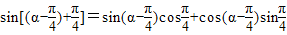 =
=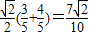
∴
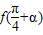 =
=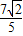
解法2:依题意得:
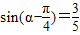 ,得
,得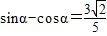 ----①
----①∵
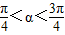 .∴
.∴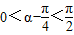 ,∴
,∴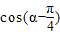 =
=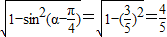
由
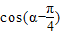 =
= 得
得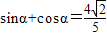 -----------②
-----------②①+②得
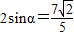 ,∴
,∴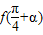 =
=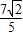
解法3:由
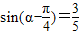 得
得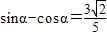 ,
,两边平方得,
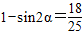 ,
,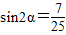 ,
,∵
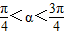 .∴
.∴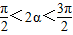 由
由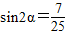 >0知
>0知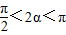
∴
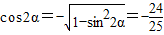 ,由cos2α=1-2sin2α,得
,由cos2α=1-2sin2α,得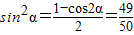
∴
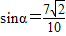 ∴
∴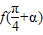 =
=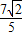 .
.点评:本题考查正弦函数性质,解决的方法灵活,解法一侧重拼凑角的方法,考查两角和的正弦公式的应用,解法二侧重方程组思想方法,解法三侧重于倍角公式,升幂公式的考查,属于中档题.

练习册系列答案
相关题目
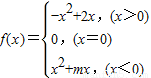 ,
, ;
; 的图象;
的图象; 在区间[-1,|
在区间[-1,| |-2]上单调递增,试确定
|-2]上单调递增,试确定 .
. 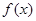 的最小正周期和当
的最小正周期和当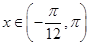 时的值域;
时的值域;
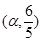 ,
,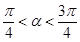 .求
.求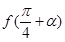 的值.
的值. .
. 的值;
的值; ,
, ,求
,求 的值.
的值. ,函数
,函数 .
. 的单调递减区间;
的单调递减区间; 在区间
在区间 上有极值,求
上有极值,求 的取值范围;
的取值范围;