题目内容
设数列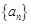 的前
的前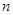 项和为
项和为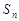 ,若对任意
,若对任意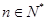 ,都有
,都有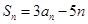 .
.
⑴求数列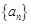 的首项;
的首项;
⑵求证:数列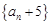 是等比数列,并求数列
是等比数列,并求数列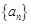 的通项公式;
的通项公式;
⑶数列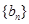 满足
满足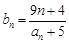 ,问是否存在
,问是否存在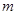 ,使得
,使得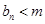 恒成立?如果存在,求出
恒成立?如果存在,求出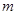 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
【答案】
⑴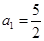 ;⑵
;⑵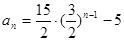 ;⑶
;⑶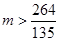 。
。
【解析】
试题分析:⑴∵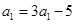 ∴
∴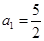 3分
3分
⑵∵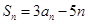 ∴
∴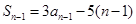 (
(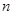 ≥2)
≥2)
∴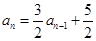 5分
5分
∴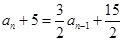

∴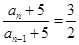 (为常数) (
(为常数) (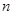 ≥2)
≥2)
∴数列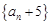 是以
是以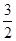 为公比的等比数列
7分
为公比的等比数列
7分
∴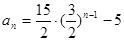 10分
10分
⑶∵ ∴
∴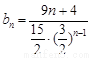
∴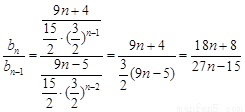 12分
12分
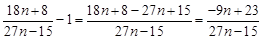 14分
14分
∴当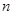 ≥3时,
≥3时,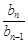 <1; 当
<1; 当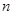 =2时,
=2时,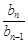 >1
>1
∴当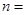 2时,
2时,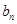 有最大值
有最大值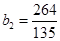
∴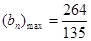 15分
15分
∴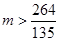 16分
16分
考点:本题主要考查等差数列、等比数列的的基础知识,函数的单调性。
点评:中档题,本题具有较强的综合性,本解答根据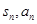 的关系确定通项公式,认识到数列的特征。对于存在性问题,往往先假设存在,本题通过考察
的关系确定通项公式,认识到数列的特征。对于存在性问题,往往先假设存在,本题通过考察 的单调性,利用“放缩法”,证明假设的合理性。
的单调性,利用“放缩法”,证明假设的合理性。

练习册系列答案
相关题目
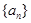 中,若任意两个不等的正整数
中,若任意两个不等的正整数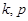 ,都有
,都有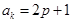 ,
,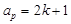 ,设数列
,设数列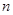 项和为
项和为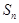 ,若
,若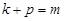 ,则
,则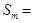 (结果用
(结果用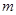 表示)。
表示)。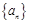 的前
的前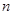 项和为
项和为 ,若
,若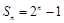 ,则
,则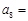
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的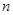
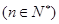 都有
都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时,
时, 的周期数列;当
的周期数列;当 时,
时, 是周期为
是周期为 的周期数列。设数列
的周期数列。设数列 满足
满足
 .
. 的周期数列,则常数
的周期数列,则常数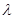 的值是
;
的值是
; ,若
,若 ,则
,则 .
. 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.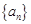 的前
的前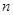 项和为
项和为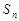 ,若对任意
,若对任意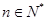 ,都有
,都有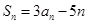 .
.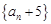 是等比数列,并求数列
是等比数列,并求数列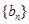 满足
满足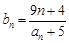 ,问是否存在
,问是否存在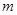 ,使得
,使得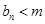 恒成立?如果存在,求出
恒成立?如果存在,求出