题目内容
(本小题满分12分)
已知双曲线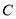 :
: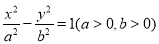 的一条渐近线为
的一条渐近线为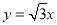 ,右焦点
,右焦点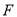 到直线
到直线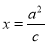 的距离为
的距离为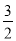 .
.
(1)求双曲线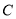 的方程;
的方程;
(2)斜率为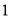 且在
且在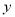 轴上的截距大于
轴上的截距大于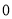 的直线
的直线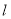 与曲线
与曲线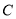 相交于
相交于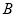 、
、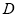 两点,已知
两点,已知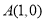 ,若
,若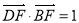 证明:过
证明:过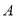 、
、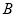 、
、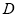 三点的圆与
三点的圆与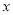 轴相切.
轴相切.
(1) ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)设双曲线的方程,若焦点明确,设双曲线的标准方程,结合条件用待定系数法求出 的值,若不明确,需分焦点在
的值,若不明确,需分焦点在 轴和
轴和 轴上两种情况讨论;(2)解决直线和双曲线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与双曲线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
轴上两种情况讨论;(2)解决直线和双曲线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与双曲线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(1)依题意有 ,
,
∵
∴
∴ ,
,
∴
∴曲线 的方程为
的方程为 6分
6分
(2)设直线 的方程为
的方程为 ,则
,则 ,
, ,
, 的中点为
的中点为
由 得
得 
∴ ,
,
∵ ,即
,即
∴ (舍)或
(舍)或
∴ ,
,
 点的横坐标为
点的横坐标为
∵

∴
∴过 、
、 、
、 三点的圆以点
三点的圆以点 为圆心,
为圆心, 为直径
为直径
∵ 点的横坐标为
点的横坐标为
∴
∵
∴过 、
、 、
、 三点的圆与
三点的圆与 轴相切 12分
轴相切 12分
考点:1、双曲线的标准方程;2、双曲线的综合问题.
考点分析: 考点1:双曲线的标准方程 考点2:双曲线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
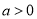 ,函数
,函数 ,
,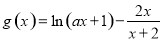 .
.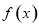 在
在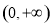 上的单调性;
上的单调性;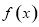 在
在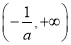 上存在两个极值点
上存在两个极值点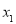 ,
,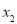 ,且
,且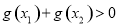 ,求常数
,求常数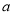 的取值范围.
的取值范围. 为虚数单位,则
为虚数单位,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 , 则判断框中应填
, 则判断框中应填
 B.
B.
 D.
D.
 ,
, ,则
,则
 B.
B. C.
C. D.
D.
 有两个极值点,则实数
有两个极值点,则实数 的取值范围是 .
的取值范围是 .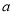 ,
,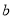 是两条不同的直线,
是两条不同的直线,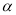 ,
,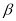 是两个不同的平面,
是两个不同的平面, ,
,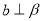 ,则
,则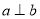 的
的 y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥P F2,则
y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥P F2,则 中,内角
中,内角 所对的边分别为
所对的边分别为 ,
, .
. 的大小;
的大小; 的角平分线
的角平分线 交线段
交线段 于
于 ,且
,且 ,设
,设 .
. 与
与 的关系式;
的关系式; 和
和 的面积分别为
的面积分别为 、
、 ,问当
,问当 取何值时,
取何值时, +
+ 的值最小,最小值是多少?
的值最小,最小值是多少?