题目内容
设等差数列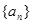 的公差
的公差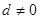 ,等比数列
,等比数列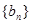 为公比为
为公比为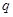 ,且
,且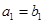 ,
,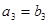 ,
,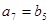 .
.
(1)求等比数列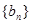 的公比
的公比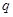 的值;
的值;
(2)将数列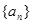 ,
,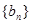 中的公共项按由小到大的顺序排列组成一个新的数列
中的公共项按由小到大的顺序排列组成一个新的数列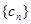 ,是否存在正整数
,是否存在正整数 (其中
(其中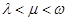 )使得
)使得 和
和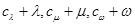 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1) (2)不存在
(2)不存在 满足题意
满足题意
【解析】
试题分析:解:(1)设 =
= ,由题意
,由题意
 即
即

 不合题意 3分
不合题意 3分
故 ,解得
,解得
 5分
5分
(2)答:不存在正整数 (其中
(其中 )使得
)使得 和
和 均构成等差数列
均构成等差数列
证明:假设存在正整数 满足题意
满足题意
设 =
= 且
且 ,故
,故  ,
,
又
 -
-
 即
即 7分
7分


 8分
8分
令 ,则
,则
 10分
10分
若存在正整数 满足题意,则
满足题意,则

 ,又
,又
又 ,
, 12分
12分
又 在R上为增函数,
在R上为增函数, 。与题设
。与题设 矛盾,
矛盾,
 假设不成立
假设不成立
故不存在 满足题意. 14分
满足题意. 14分
考点:等差数列和等比数列的运用
点评:主要是考查了基本的数列的通项公式和运用数列与函数的单调性的关系来证明不等式。属于中档题。

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 的公差
的公差 ≠0,
≠0, .若
.若 是
是 与
与 的等比中项,则
的等比中项,则 ( )
( ) 的公差d不为0,
的公差d不为0, ,若
,若 是
是 与
与 的等比中项,则k=( )
的等比中项,则k=( ) 的公差
的公差 ≠0,
≠0, .若
.若 是
是 与
与 的等比中项,则
的等比中项,则
 的公差
的公差 ≠0,
≠0, .若
.若 是
是 与
与 的等比中项,则
的等比中项,则