Question

轴截面为正三角形的圆锥内有一个内切球，若圆锥的底面半径为1cm，求球的体积．（提示：可考虑轴截面）

Answer 1

分析：作出轴截面，利用Rt△AOE∽Rt△ACD，并且设出OE=R，求出R，然后求出球的体积．

解答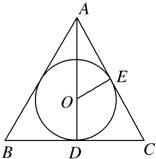：解：如图作出轴截面，
∵△ABC是正三角形，
∴CD=

1

2

AC．
∵CD=1 cm，
∴AC=2 cm，AD=

3

 cm．
∵Rt△AOE∽Rt△ACD，
∴

OE

AO

=

CD

AC

．
设OE=R，则AO=

3

-R，
∴

R

3 -R

=

1

2

，
∴R=

3

3

（cm）．
∴V球=

4

3

π（

3

3

）³=

4 3

27

π（cm³）．
∴球的体积等于

4 3

27

π cm³．

点评：本题考查球内接多面体，球的体积的求法，考查空间想象能力以及计算能力．