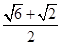题目内容
函数
 在区间
在区间 上单调递减,且函数值从1减小到
上单调递减,且函数值从1减小到 ,那么此函数图象与
,那么此函数图象与 轴交点的纵坐标为( )
轴交点的纵坐标为( )
A. | B. | C. | D. |
A
解析试题分析:依题意,利用正弦函数的单调性可求得y=sin(ωx+φ)的解析式,从而可求得此函数图象与y轴交点的纵坐标.解:∵函数y=sin(ωx+φ)在区间 上单调递减,且函数值从1减小到-1,
上单调递减,且函数值从1减小到-1, ∴
∴
∴T=π,又T= ∴ω=2又sin(2×
∴ω=2又sin(2× +φ)=1,∴
+φ)=1,∴ +φ=2kπ+
+φ=2kπ+ ,k∈Z.∴φ=2kπ+
,k∈Z.∴φ=2kπ+ ,k∈Z.∵|φ|<
,k∈Z.∵|φ|< ,∴φ=
,∴φ=
∴y=sin(2x+ ),令x=0,有y=sin
),令x=0,有y=sin =
= ∴此函数图象与y轴交点的纵坐标为
∴此函数图象与y轴交点的纵坐标为 故选A.
故选A.
考点:三角函数图像
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得ω与φ的值是关键,也是难点,考查分析与理解应用的能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
函数 的部分图象如图
的部分图象如图
所示,则
A. |
B. |
C. |
D. |
函数 在一个周期内的图象如右,则此函数的解析式为( )
在一个周期内的图象如右,则此函数的解析式为( )
A. | B. |
C. | D. |
使函数 为奇函数,且在
为奇函数,且在 上是减函数的
上是减函数的 的一个值是( )
的一个值是( )
A. | B. | C.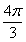 | D. |
若 ,则
,则
A. | B. |
C. | D. |
函数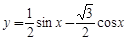 的最小正周期是( )
的最小正周期是( )
A. | B. | C. | D. |
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
 的图形按向量
的图形按向量 平移后得到函数
平移后得到函数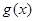 的图形,满足
的图形,满足 ,则向量
,则向量 的一个可能值是( )
的一个可能值是( )



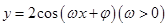 且
且 在区间
在区间 上单调递增,且函数值从
上单调递增,且函数值从 增大到
增大到 ,那么函数图像与
,那么函数图像与 轴交点的纵坐标为( )
轴交点的纵坐标为( )