Question

（本小题满分12分）

已知等比数列{a_n}的前n项和A_n=，数列{b_n}(b_n＞0)的首项为b₁=a，且前n项和S_n满足S_n-S_n-1=；

（1）求数列{a_n}和{b_n}的通项公式；

（2）若数列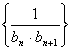的前n项和为T_n，判断T_n+a_n(b_n+1)与0的大小。

Answer 1

解：（1）a₁=–a，a₂=A₂–A₁= –，a₃=A₃–A₂=–，

又数列{a_n}成等比数列，∴ a₂²=a₁a₃，即=(–a)∙( –)∴a=1，又公比q==,

∴a_n== –2

∵S_n-S_n-1=

又b_n＞0，数列{}是首相为1，公差为1的等差数列，

当n=1时，b₁=1；当n≥2时，b_n=S_n–S_n-1=n²-(n-1)²=2n-1

所以b_n=2n-1。

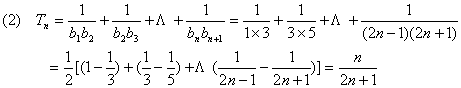
T_n+a_n(b_n+1)=-2n´2()ⁿ=

当n=1 、2、3时，T_n+a_n(b_n+1)<0，

当n≥4时，T_n+a_n(b_n+1)>0，即n≥4时，3ⁿ>4(2n+1)，下用数学归纳法证明：

当n=4时，3⁴=81，而4（2´4+1）=36，∴n=4时，3ⁿ>4(2n+1)。

假设n=k(k≥4)时，不等式成立，即：；

则n=k+1时，3^k+1>3´4(2k+1)=4(6k+3)>4(2k+3)=4[2(k+1)+1]，即：n=k+1时，不等式成立。

综上可知：n≥4时，3ⁿ>4(2n+1)。

故当n=1 、2、3时，T_n+a_n(b_n+1)<0；

当n≥4时，3ⁿ>4(2n+1)。