题目内容
正四棱锥底面边长为4,侧棱长为3,则其侧面积为________.
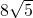
分析:求出正四棱锥的斜高,然后求出侧面积即可.
解答:因为正四棱锥底面边长为4,侧棱长为3,所以正四棱锥的斜高为:
 =
= .
.所以正四棱锥的侧面积为:
 =8
=8 .
.故答案为:8
 .
.点评:本题考查几何体的侧面积的求法,考查计算能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
题目内容
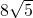
 =
= .
. =8
=8 .
. .
.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案