题目内容
8．求值：$sin40°（\sqrt{3}-tan10°）$=1．分析 由条件利用三角函数的恒等变换化简可得结果．
解答 解：$sin40°（\sqrt{3}-tan10°）$=sin40°•$\frac{\sqrt{3}cos10°-sin10°}{cos10°}$=sin40°•$\frac{2•cos（30°+10°）}{cos10°}$=$\frac{2sin40°cos40°}{cos10°}$=$\frac{sin80°}{cos10°}$=1，
故答案为：1．
点评 本题主要考查三角函数的恒等变换及化简求值，属于基础题．
练习册系列答案
相关题目
19．设F1、F2是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的两个焦点，点P在双曲线上，且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，则|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|的值为（ ）
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 4 | D． | 8 |
16．为了测得河对岸塔AB的高度，先在河岸上选一点C，使C在塔底B的正东方向上，此时测得塔顶A的仰角为60°．再由点C沿北偏东15°方向走了20米到达点D，测得∠BDC=45°，则塔AB的高度为（ ）
| A． | 20$\sqrt{6}$米 | B． | 20$\sqrt{3}$米 | C． | 20$\sqrt{2}$米 | D． | 20米 |
13．
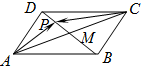如图，平行四边形ABCD的两条对角线相交于点M，点P是MD中点，若|$\overrightarrow{AB}$|=2，|$\overrightarrow{AD}$|=1，且∠BAD=60°，则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为（ ）
如图，平行四边形ABCD的两条对角线相交于点M，点P是MD中点，若|$\overrightarrow{AB}$|=2，|$\overrightarrow{AD}$|=1，且∠BAD=60°，则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为（ ）| A． | -$\frac{5}{16}$ | B． | -$\frac{15}{16}$ | C． | -$\frac{25}{16}$ | D． | -$\frac{27}{16}$ |
20．曲线x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{5}x}\\{y′=\frac{1}{3}y}\end{array}\right.$后，变成的曲线方程是（ ）
| A． | 25x2+9y2=1 | B． | 9x2+25y2=1 | C． | 25x+9y=1 | D． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
18．已知等差数列{an}的通项公式an=2-2n，则它的公差为（ ）
| A． | -2 | B． | 3 | C． | 2 | D． | -3 |