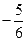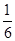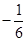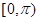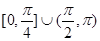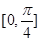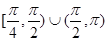题目内容
已知点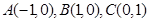 ,直线
,直线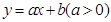 将△
将△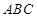 分割为面积相等的两部分,则
分割为面积相等的两部分,则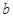 的取值范围是( )
的取值范围是( )
A.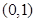 | B.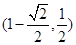 | C.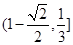 | D.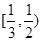 |
B
解析试题分析:由题意可得,三角形ABC的面积为 S= 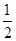 •AB•OC=1,
•AB•OC=1,
由于直线y=ax+b(a>0)与x轴的交点为M(?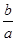 ,0),由?
,0),由?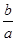 ≤0可得点M在射线OA上.
≤0可得点M在射线OA上.
设直线和BC的交点为 N,则由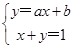 ,可得点N的坐标为(
,可得点N的坐标为( ),
),
若点M和点A重合,则点N为线段BC的中点,则?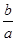 =-1,且
=-1,且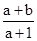 =
=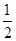 ,解得a=b=
,解得a=b=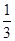 ,
,
若点M在点O和点A之间,则点N在点B和点C之间,由题意可得三角形NMB的面积等于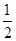 ,即
,即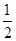 •MB•
•MB•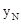 =
=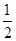 ,
,
即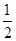 •
•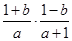 =
=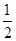 ,解得a=
,解得a=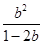 >0,故b<
>0,故b<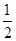 ,
,
若点M在点A的左侧,则?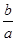 <-1,b<a,设直线y=ax+b和AC的交点为P,
<-1,b<a,设直线y=ax+b和AC的交点为P,
则由 求得点P的坐标为(
求得点P的坐标为(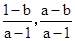 ),
),
此时,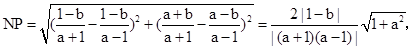 ,
,
此时,点C(0,1)到直线y=ax+b的距离等于 ,
,
由题意可得,三角形CPN的面积等于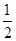 ,即
,即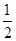 •
•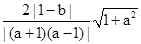 •
• =
=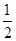 ,
,
化简可得2(1-b)2=|a2-1|.
由于此时 0<b<a<1,∴2(1-b)2=|a2-1|=1-a2 .
两边开方可得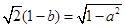 <1,则1-b<
<1,则1-b<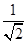 ,即b>1?
,即b>1?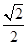 ,
,
综合以上可得,b=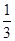 可以,且b<
可以,且b<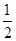 ,且b>1?
,且b>1?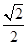 ,即b的取值范围是(1?
,即b的取值范围是(1?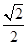 ,
,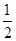 )。
)。
选B。
考点:直线方程,三角形面积,不等式的性质
点评:难题,本题综合性较强,综合考查直线方程,三角形面积,不等式的性质,注意分析图形的可能情况,做到不重不漏。

 名校课堂系列答案
名校课堂系列答案若直线过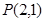 点且在两坐标轴上的截距相等,则这样的直线有几条( )
点且在两坐标轴上的截距相等,则这样的直线有几条( )
| A.1条 | B.2 条 | C.3条 | D.以上都有可能 |
已知点(a,2) (a>0)到直线l: x y+3=0的距离为1, 则a的值为( )
A.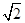 | B. 2 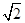 | C.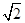 +1 +1 | D.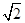 1 1 |
已知点(a,2) (a>0)到直线l: x-y+3=0的距离为1, 则a的值为( )
A. | B. 2-  | C. -1 -1 | D. +1 +1 |
直线l经过原点和点(-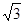 , 1),则它的斜率为
, 1),则它的斜率为
A.-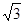 | B.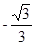 | C.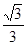 | D.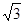 |
已知两条直线y= x-2和y=(
x-2和y=( +2)x+1互相垂直,则
+2)x+1互相垂直,则 等于 ( )
等于 ( )
| A.2 | B.1 | C.0 | D.-1 |
若直线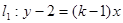 和直线
和直线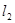 关于直线
关于直线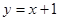 对称,那么直线
对称,那么直线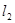 恒过定点( )
恒过定点( )
| A.(2,0) | B.(1,-1) | C.(1,1) | D.(-2,0) |