题目内容
已知函数f(x)为定义在R上的奇函数,且当x>0时,函数f(x)=x2-2x.
(1)试求函数f(x)的解析式;
(2)试求函数f(x)在x∈[0,3]上的值域.
(1)试求函数f(x)的解析式;
(2)试求函数f(x)在x∈[0,3]上的值域.
(1)令x<0,则-x>0,
∵x>0时,f(x)=x2-2x,
∴f(-x)=(-x)2-2(-x)=x2+2x,
又f(x)为定义在R上的奇函数,
∴f(-x)=-f(x)=-x2-2x.
当x=0时,f(x)=x2-2x=0,
∴f(x)=
.
(2)x∈[0,3]时,f(x)=x2-2x,
∵对称轴方程为x=1,抛物线开口向上,
∴f(x)=x2-2x在[0,3]上的最小值和最大值分别为:
f(x)min=f(1)=1-2=-1,
f(x)max=f(3)=9-6=3.
∴函数f(x)在x∈[0,3]上的值域为[-1,3].
∵x>0时,f(x)=x2-2x,
∴f(-x)=(-x)2-2(-x)=x2+2x,
又f(x)为定义在R上的奇函数,
∴f(-x)=-f(x)=-x2-2x.
当x=0时,f(x)=x2-2x=0,
∴f(x)=
|
(2)x∈[0,3]时,f(x)=x2-2x,
∵对称轴方程为x=1,抛物线开口向上,
∴f(x)=x2-2x在[0,3]上的最小值和最大值分别为:
f(x)min=f(1)=1-2=-1,
f(x)max=f(3)=9-6=3.
∴函数f(x)在x∈[0,3]上的值域为[-1,3].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 = .
= .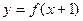 的图像与函数
的图像与函数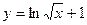 的图像关于直线
的图像关于直线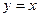 对称,则
对称,则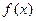 =( )
=( )



 是定义在R上的连续函数,且
是定义在R上的连续函数,且 ,则
,则 ( )
( )
 ,则
,则 .
.