Question

设变量x，y满足约束条件

x≥0 x+2y≥4 2x+y≤4

，则z=3x-y的最小值为

-4

．

Answer 1

分析：先根据条件画出可行域，设z=3x-y，则可得y=3x-Z，将最小值转化为y轴上的截距最大，根据图象可判断，过可行域内的点B（1，1）时，截距最大，从而得到z最小值即可．

解答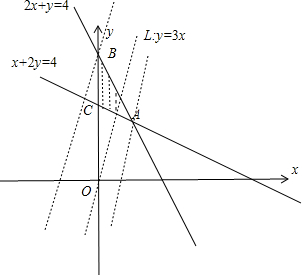：解：∵变量x，y满足约束条件

x≥0 x+2y≥4 2x+y≤4

，在坐标系中画出可行域三角形，
作直线L：3x-y=0经过点B时，在y轴上的截距最大，次数z最小，
由

2x+y=4 x=0

可得B（0，4），Z=-4
∴z=3x-y的最小值为-4．
故答案为：-4．

点评：本题主要考查了求解目标函数的最值，用几何方法处理代数问题，体现了数形结合思想、化归思想．