题目内容
已知函数f(x)=2x-π,g(x)=cosx.
(Ⅰ)设h(x)=f(x)-g(x),若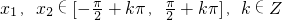 ,试比较
,试比较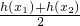 与
与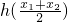 的大小关系;
的大小关系;
(Ⅱ)若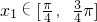 且f(xn+1)=g(xn).求证:
且f(xn+1)=g(xn).求证: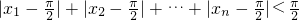 .
.
解:(Ⅰ)h(x)=2x-π-cosx.∴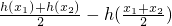
=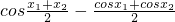 .(2分)
.(2分)
令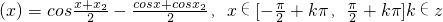 .
.
则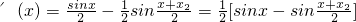 .
.
又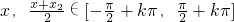 .
.
∴当k为偶数时,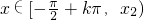 时,?'(x)<0.
时,?'(x)<0.
x∈ 时,?'(x)>0.(5分)
时,?'(x)>0.(5分)
∴?(x)>?(x2)=0.∴从而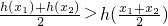 .(6分)
.(6分)
同理可得当k为奇数时, .
.
∴当k为偶数时,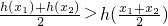 ,
,
当k为奇数时, .(7分)
.(7分)
(Ⅱ)由条件知:2xn+1-π=cosxn.
当 ,当
,当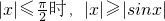 ,∴x∈R时恒有|x|≥|sinx|.(9分)
,∴x∈R时恒有|x|≥|sinx|.(9分)
故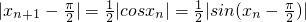
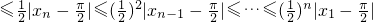 .
.
又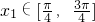 ,∴
,∴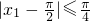 .∴
.∴
=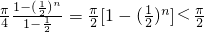 .(14分)
.(14分)
分析:(I)h(x)=2x-π-cosx,令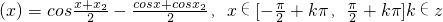 .然后利用导数研究函数的最小值,讨论k的奇偶,即可得到
.然后利用导数研究函数的最小值,讨论k的奇偶,即可得到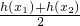 与
与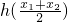 的大小关系;
的大小关系;
(II)由条件知:2xn+1-π=cosxn,则x∈R时恒有|x|≥|sinx|,从而得到 ,然后利用等比数列求和公式进行求和即可证得结论.
,然后利用等比数列求和公式进行求和即可证得结论.
点评:本题主要考查了利用导数证明不等式,以及数列与不等式的综合,同时考查了分类讨论的数学思想,属于中档题.
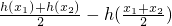
=
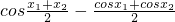 .(2分)
.(2分)令
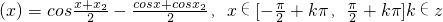 .
.则
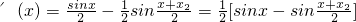 .
.又
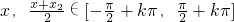 .
.∴当k为偶数时,
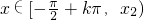 时,?'(x)<0.
时,?'(x)<0.x∈
 时,?'(x)>0.(5分)
时,?'(x)>0.(5分)∴?(x)>?(x2)=0.∴从而
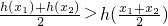 .(6分)
.(6分)同理可得当k为奇数时,
 .
.∴当k为偶数时,
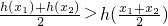 ,
,当k为奇数时,
 .(7分)
.(7分)(Ⅱ)由条件知:2xn+1-π=cosxn.
当
 ,当
,当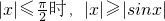 ,∴x∈R时恒有|x|≥|sinx|.(9分)
,∴x∈R时恒有|x|≥|sinx|.(9分)故
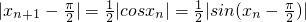
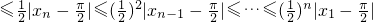 .
.又
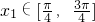 ,∴
,∴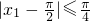 .∴
.∴
=
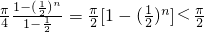 .(14分)
.(14分)分析:(I)h(x)=2x-π-cosx,令
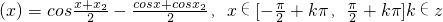 .然后利用导数研究函数的最小值,讨论k的奇偶,即可得到
.然后利用导数研究函数的最小值,讨论k的奇偶,即可得到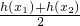 与
与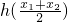 的大小关系;
的大小关系;(II)由条件知:2xn+1-π=cosxn,则x∈R时恒有|x|≥|sinx|,从而得到
 ,然后利用等比数列求和公式进行求和即可证得结论.
,然后利用等比数列求和公式进行求和即可证得结论.点评:本题主要考查了利用导数证明不等式,以及数列与不等式的综合,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目