题目内容
已知函数f(x)=ax2+2ln(1-x)(a∈R).
(Ⅰ)若f(x)在[-3,-2)上是增函数,求实数a的取值范围;
(Ⅱ)是否存在正实数a,使得f(x)的导函数f′(x)有最大值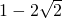 ?若存在,求出a的值;若不存在,请说明理由.
?若存在,求出a的值;若不存在,请说明理由.
解:(Ⅰ)由已知得f(x)的定义域为(-∞,1)
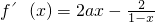 .(2分)
.(2分)
由题意得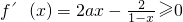 对一切x∈[-3,-2)恒成立,
对一切x∈[-3,-2)恒成立,
∴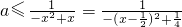 .(5分)
.(5分)
当x∈[-3,-2)时, ,
,
∴ .故
.故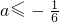 .(7分)
.(7分)
(Ⅱ)假设存在正实数a,使得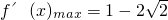 成立.
成立. .(9分)
.(9分)
由 ,得
,得 ,
,
∴ .由于
.由于 ,故应舍去.
,故应舍去.
当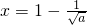 时,
时, .(11分)
.(11分)
令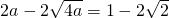 ,解得
,解得 或
或 .(13分)
.(13分)
另解:假设存在正实数a,使得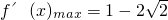 成立.
成立.
设 ,则
,则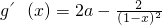 .(9分)
.(9分)
由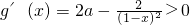 ,解得
,解得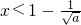 或
或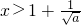 .
.
因为x∈(-∞,1),
∴g(x)在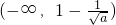 上单调递增,在上单调递减.
上单调递增,在上单调递减.
∴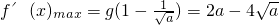 .(11分)
.(11分)
令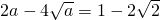 ,解得
,解得 或
或 .(14分)
.(14分)
分析:(Ⅰ)求出函数的定义域,求出函数的导数,利用导数在[-3,-2)恒为正,通过二次函数的最值求出实数a的取值范围;
(Ⅱ)假设存在正实数a,使得f(x)的导函数f′(x)有最大值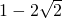 ,直接求出a的值.
,直接求出a的值.
另解:假设存在正实数a,使得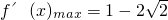 成立.设
成立.设 ,求出
,求出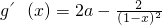 >0,解得
>0,解得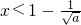 或
或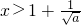 .通过x∈(-∞,1),g(x)在
.通过x∈(-∞,1),g(x)在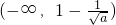 上单调递增,在上单调递减.得到
上单调递增,在上单调递减.得到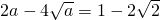 ,解得
,解得 或
或 .
.
点评:本题只要考查求函数的导数以及函数的最值问题,体现转化的数学思想,特别注意新变量的取值范围,同时也考查了二次函数在定区间上的最值问题,恒成立问题,属中档题.
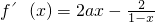 .(2分)
.(2分)由题意得
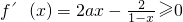 对一切x∈[-3,-2)恒成立,
对一切x∈[-3,-2)恒成立,∴
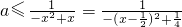 .(5分)
.(5分)当x∈[-3,-2)时,
 ,
,∴
 .故
.故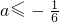 .(7分)
.(7分)(Ⅱ)假设存在正实数a,使得
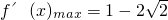 成立.
成立. .(9分)
.(9分)由
 ,得
,得 ,
,∴
 .由于
.由于 ,故应舍去.
,故应舍去.当
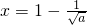 时,
时, .(11分)
.(11分)令
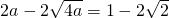 ,解得
,解得 或
或 .(13分)
.(13分)另解:假设存在正实数a,使得
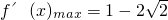 成立.
成立.设
 ,则
,则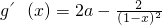 .(9分)
.(9分)由
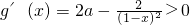 ,解得
,解得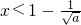 或
或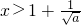 .
.因为x∈(-∞,1),
∴g(x)在
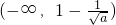 上单调递增,在上单调递减.
上单调递增,在上单调递减.∴
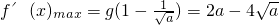 .(11分)
.(11分)令
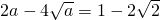 ,解得
,解得 或
或 .(14分)
.(14分)分析:(Ⅰ)求出函数的定义域,求出函数的导数,利用导数在[-3,-2)恒为正,通过二次函数的最值求出实数a的取值范围;
(Ⅱ)假设存在正实数a,使得f(x)的导函数f′(x)有最大值
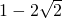 ,直接求出a的值.
,直接求出a的值.另解:假设存在正实数a,使得
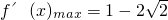 成立.设
成立.设 ,求出
,求出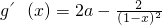 >0,解得
>0,解得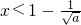 或
或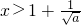 .通过x∈(-∞,1),g(x)在
.通过x∈(-∞,1),g(x)在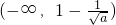 上单调递增,在上单调递减.得到
上单调递增,在上单调递减.得到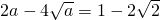 ,解得
,解得 或
或 .
.点评:本题只要考查求函数的导数以及函数的最值问题,体现转化的数学思想,特别注意新变量的取值范围,同时也考查了二次函数在定区间上的最值问题,恒成立问题,属中档题.

练习册系列答案
相关题目