题目内容
已知 ,且
,且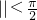 ,则tanφ=
,则tanφ=
- A.

- B.

- C.

- D.

D
分析:首先根据 ,结合两角差的余弦公式,展开可得sin?=
,结合两角差的余弦公式,展开可得sin?= ,再由
,再由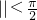 ,sin?>0,可得?=
,sin?>0,可得?= ,所以
,所以
tanφ= ,从而得到正确选项.
,从而得到正确选项.
解答:∵ ,
,
∴ ,即sin?=
,即sin?=
又∵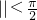 ,sin?=
,sin?= >0
>0
∴?为锐角,且?= ,可得tanφ=
,可得tanφ=
故选D
点评:本题给出 的余弦,欲求?的正切值,着重考查了特殊角的三角函数和同角三角函数的关系等知识点,属于基础题.
的余弦,欲求?的正切值,着重考查了特殊角的三角函数和同角三角函数的关系等知识点,属于基础题.
分析:首先根据
 ,结合两角差的余弦公式,展开可得sin?=
,结合两角差的余弦公式,展开可得sin?= ,再由
,再由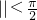 ,sin?>0,可得?=
,sin?>0,可得?= ,所以
,所以tanφ=
 ,从而得到正确选项.
,从而得到正确选项.解答:∵
 ,
,∴
 ,即sin?=
,即sin?=
又∵
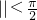 ,sin?=
,sin?= >0
>0∴?为锐角,且?=
 ,可得tanφ=
,可得tanφ=
故选D
点评:本题给出
 的余弦,欲求?的正切值,着重考查了特殊角的三角函数和同角三角函数的关系等知识点,属于基础题.
的余弦,欲求?的正切值,着重考查了特殊角的三角函数和同角三角函数的关系等知识点,属于基础题. 
练习册系列答案
相关题目
 ,且
,且 ,则tanθ= .
,则tanθ= .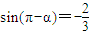 ,且
,且 ,则tan(2π-α)的值为( )
,则tan(2π-α)的值为( )