题目内容
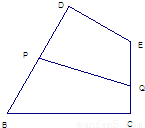
如图,有一块四边形BCED绿化区域,其中∠C=∠D=90°,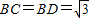 ,CE=DE=1,现准备经过DB上一点P和EC上一点Q铺设水管PQ,且PQ将四边形BCED分成面积相等的两部分,设DP=x,EQ=y.
,CE=DE=1,现准备经过DB上一点P和EC上一点Q铺设水管PQ,且PQ将四边形BCED分成面积相等的两部分,设DP=x,EQ=y.(1)求x,y的关系式; (2)求水管PQ的长的最小值.
【答案】分析:(1)延长BD、CE交于A,利用S△ADE=S△BDE=S△BCE= ,S△APQ=
,S△APQ= 可建立x,y的关系式;
可建立x,y的关系式;
(2)利用余弦定理表示出PQ,再借助于基本不等式求出水管PQ的长的最小值.
解答:解:(1)延长BD、CE交于A,则AD= ,AE=2 则S△ADE=S△BDE=S△BCE=
,AE=2 则S△ADE=S△BDE=S△BCE=
∵S△APQ= ,∴
,∴ ∴
∴

(2)PQ2=AP2+AQ2-2AP•AQcos30°
= •
•
当 ,即
,即 ,
,
点评:本题主要考查变量关系,考查余弦定理及基本不等式的运用,有一定的综合性.
 ,S△APQ=
,S△APQ= 可建立x,y的关系式;
可建立x,y的关系式; (2)利用余弦定理表示出PQ,再借助于基本不等式求出水管PQ的长的最小值.
解答:解:(1)延长BD、CE交于A,则AD=
 ,AE=2 则S△ADE=S△BDE=S△BCE=
,AE=2 则S△ADE=S△BDE=S△BCE=
∵S△APQ=
 ,∴
,∴ ∴
∴

(2)PQ2=AP2+AQ2-2AP•AQcos30°
=
 •
•
当
 ,即
,即 ,
,
点评:本题主要考查变量关系,考查余弦定理及基本不等式的运用,有一定的综合性.

练习册系列答案
相关题目
 如图,某花木场有一块等腰梯形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )
如图,某花木场有一块等腰梯形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )