题目内容
已知a,b是正常数,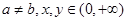 ,求证:
,求证: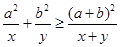 ,指出等号成立的条件;(2)利用(1)的结论求函数
,指出等号成立的条件;(2)利用(1)的结论求函数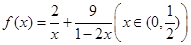 的最小值,指出取最小值时x的值.
的最小值,指出取最小值时x的值.
(1)当 时取等号;(2)当
时取等号;(2)当 时,
时, .
.
解析试题分析:解题思路:(1)设法出现定积,利用基本不等式证明;(2)将 配成(1)中的形式.
配成(1)中的形式.
规律总结:利用基本不等式求最值问题,关键要出现定值(已知 若
若 ,则
,则 ;
;
若 ,则
,则 .注意点:利用基本不等式求最值问题,要注意其使用条件(一正、二定、三等号).
.注意点:利用基本不等式求最值问题,要注意其使用条件(一正、二定、三等号).
试题解析:(1)应用均值不等式,得
 ,故
,故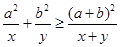 .
.
当且仅当 ,即
,即 时上式取等号.
时上式取等号.
(2)由(1), (当且仅当
(当且仅当 ,
,
即 时上式取等号),即
时上式取等号),即 .
.
考点:基本不等式.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 ,其中
,其中 ,求
,求 的最小值,及此时
的最小值,及此时 与
与 的值.
的值.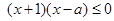 ,讨论
,讨论 求证:
求证: .
. ,且
,且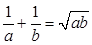 .
. 的最小值;
的最小值; ,使得
,使得 ?并说明理由.
?并说明理由.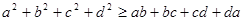
 ,
, ,且
,且 ,则
,则 的最大值为 .
的最大值为 . ,则
,则 的最小值为 ※
的最小值为 ※  恒成立,则a的取值范围是 。
恒成立,则a的取值范围是 。 +
+ 的最大值;
的最大值; +
+ 最大值为2
最大值为2 ,求正数a的值.
,求正数a的值.