题目内容
已知数列an满足a1=1,n≥2时, .
.
(1)求证:数列 为等差数列;
为等差数列;
(2)求 的前n项和.
的前n项和.
解:(1)证明:由已知 .
.
整理可得an-1-an=2an-1an(n≥2),
同时除以anan-1可得 ,
,
所以 为首项为
为首项为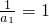 ,公差为2的等差数列.
,公差为2的等差数列.
(2)解:由(1)可知,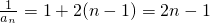 ,
,
所以 ,
,
Sn=1×3+3×32+…+(2n-1)×3n①
3Sn=1×32+3×33+…+(2n-1)×3n+1②
①-②得-2Sn=3+2×(32+33+…+3n)-(2n-1)×3n+1=(2-2n)•3n+1-6
所以得Sn=(n-1)3n+1+3
分析:要证明数列 为等差数列,只要证明可得
为等差数列,只要证明可得 ,由已知
,由已知 整理可得,
整理可得,
an-1-an=2an-1an,即 ,从而可证
,从而可证
(2)由(1)可求an,从而可得 ,利用错位相减法求数列的和即可
,利用错位相减法求数列的和即可
点评:本题主要考查了利用定义及构造法构造等差数列的形式,还考查了数列求和中的错位相减,错位相减是数列求和的考查重点及热点,但也是数列求和方法中的一个难点.
 .
.整理可得an-1-an=2an-1an(n≥2),
同时除以anan-1可得
 ,
,所以
 为首项为
为首项为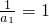 ,公差为2的等差数列.
,公差为2的等差数列.(2)解:由(1)可知,
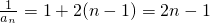 ,
,所以
 ,
,Sn=1×3+3×32+…+(2n-1)×3n①
3Sn=1×32+3×33+…+(2n-1)×3n+1②
①-②得-2Sn=3+2×(32+33+…+3n)-(2n-1)×3n+1=(2-2n)•3n+1-6
所以得Sn=(n-1)3n+1+3
分析:要证明数列
 为等差数列,只要证明可得
为等差数列,只要证明可得 ,由已知
,由已知 整理可得,
整理可得,an-1-an=2an-1an,即
 ,从而可证
,从而可证(2)由(1)可求an,从而可得
 ,利用错位相减法求数列的和即可
,利用错位相减法求数列的和即可点评:本题主要考查了利用定义及构造法构造等差数列的形式,还考查了数列求和中的错位相减,错位相减是数列求和的考查重点及热点,但也是数列求和方法中的一个难点.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目