题目内容
已知函数f(x)是定义在[a-1,2a]上的偶函数,且当x>0时,f(x)单调递增,则关于x的不等式f(x-1)>f(a)的解集为
- A.

- B.

- C.


- D.随a的值而变化
C
分析:具有奇偶性的函数定义域关于原点对称可求得a值,由偶函数性质知,f(x-1)>f(a)可化为f(|x-1|)>f( ),根据f(x)的单调性可得|x-1|>
),根据f(x)的单调性可得|x-1|> ,再考虑到定义域即可解出不等式.
,再考虑到定义域即可解出不等式.
解答:因为f(x)是定义在[a-1,2a]上的偶函数,
所以(a-1)+2a=0,解得a= .
.
则f(x)定义域为[- ,
, ].
].
由偶函数性质知,f(x-1)>f(a)可化为f(|x-1|)>f( ),
),
又x>0时,f(x)单调递增,所以|x-1|> ①,
①,
又- ≤x-1
≤x-1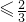 ②,
②,
联立①②解得 x<
x< 或
或 <x≤
<x≤ ,
,
故不等式f(x-1)>f(a)的解集为[ ,
, )∪(
)∪( ,
, ].
].
故选C.
点评:本题考查函数奇偶性、单调性的应用,考查抽象不等式的求解,属中等题.
分析:具有奇偶性的函数定义域关于原点对称可求得a值,由偶函数性质知,f(x-1)>f(a)可化为f(|x-1|)>f(
 ),根据f(x)的单调性可得|x-1|>
),根据f(x)的单调性可得|x-1|> ,再考虑到定义域即可解出不等式.
,再考虑到定义域即可解出不等式.解答:因为f(x)是定义在[a-1,2a]上的偶函数,
所以(a-1)+2a=0,解得a=
 .
.则f(x)定义域为[-
 ,
, ].
].由偶函数性质知,f(x-1)>f(a)可化为f(|x-1|)>f(
 ),
),又x>0时,f(x)单调递增,所以|x-1|>
 ①,
①,又-
 ≤x-1
≤x-1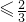 ②,
②,联立①②解得
 x<
x< 或
或 <x≤
<x≤ ,
,故不等式f(x-1)>f(a)的解集为[
 ,
, )∪(
)∪( ,
, ].
].故选C.
点评:本题考查函数奇偶性、单调性的应用,考查抽象不等式的求解,属中等题.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+