题目内容
若函数
是偶函数，则
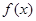的递减区间是 .
解析试题分析：解 当
时，
为一次函数，不是偶函数；当
时，得对称轴
，得
，于是
，则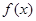的递减区间是.
考点：函数奇偶性与单调性.
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
暑假作业暑假快乐练西安出版社系列答案新活力总动员暑系列答案龙人图书快乐假期暑假作业郑州大学出版社系列答案题目内容
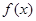若函数是偶函数，则的递减区间是 .
解析试题分析：解 当时，为一次函数，不是偶函数；当时，得对称轴，得，于是，则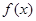的递减区间是.
考点：函数奇偶性与单调性.
暑假作业暑假快乐练西安出版社系列答案新活力总动员暑系列答案龙人图书快乐假期暑假作业郑州大学出版社系列答案
在区间
上为增函数，则
的取值范围是 __________．
,若
互不相等，且
,则
的取值范围是________________．
是任意非零常数，对于函数
有以下5个命题：
的周期函数的充要条件是
；
； 
是奇函数且是
的周期函数，则
对称；
，则
对称，关于直线
对称，则
的周期函数．
是
上的偶函数，若对于
，都有
，且当
时，
，则
=____________.
在
上有两个零点，则实数
的取值范围是________.
有一个正实根，一个负实根，则
； 
是偶函数，但不是奇函数；
定义域为R，则函数
与
的图象关于
轴对称；
和直线
的公共点个数是
，则
．其中正确的有_______________.
的交点的横坐标为
，当
时
（从>，<，=，≥，≤，无法确定，中选你认为正确的一个填到横线上）
可以表示为一个奇函数
与一个偶函数
之和，若不等式
对于
恒成立，则实数
的取值范围是____________.