题目内容
(满分14分)
已知曲线![]() .从点
.从点![]() 向曲线
向曲线![]() 引斜率为
引斜率为![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
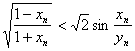 w.w.w.k.s.5.u.c
w.w.w.k.s.5.u.c
(1)求数列![]() 的通项公式;
的通项公式;
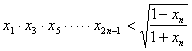
解析:(1)设直线![]() :
:![]() ,联立
,联立![]() 得
得![]() ,则
,则![]() ,∴
,∴![]() (
(![]() 舍去)
舍去)
![]() ,即
,即![]() ,∴
,∴![]()
(2)证明:∵
![]()
∴
由于 ,可令函数
,可令函数![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,给定区间
,给定区间![]() ,则有
,则有![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,即
,即![]() 在
在![]() 恒成立,又
恒成立,又![]() ,
,
则有![]() ,即
,即

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
.(本小题满分14分)
已知椭圆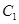 、抛物线
、抛物线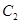 的焦点均在
的焦点均在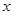 轴上,
轴上,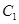 的中心和
的中心和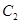 的顶点均为原点
的顶点均为原点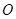 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(Ⅰ)求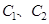 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线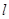 满足条件:①过
满足条件:①过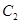 的焦点
的焦点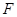 ;②与
;②与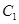 交不同两点
交不同两点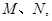 且满
且满
足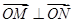 ?若存在,求出直线
?若存在,求出直线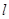 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
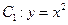 与曲线
与曲线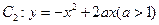 交于点O、A,直线
交于点O、A,直线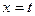 (0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
(0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。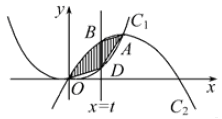
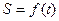 ;
;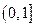 上的最大值。
上的最大值。 2
2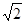
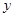
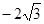
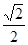
 和
和 相交于点
相交于点 且
且 ,点
,点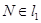 .以
.以 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到 的距离相等.若
的距离相等.若 为锐角三角形,
为锐角三角形, ,
, ,且
,且 .
. 在曲线段C上,直线
在曲线段C上,直线 ,求直线
,求直线 被圆
被圆 截得的弦长的取值范围.
截得的弦长的取值范围.
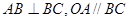 且
且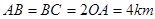 ,曲线段
,曲线段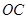 是以点
是以点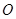 为顶点且开口向右的抛物线的一段.
为顶点且开口向右的抛物线的一段.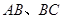 上,且一个顶点
上,且一个顶点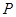 落在曲线段
落在曲线段
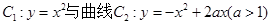 交于点O、A,直线
交于点O、A,直线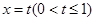 与曲线
与曲线 、
、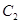 分别交于点D、B,连结OD,DA,AB.
分别交于点D、B,连结OD,DA,AB.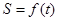 的函数表达式为
的函数表达式为 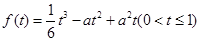

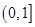 上的最大值.
上的最大值.