题目内容
已知向量 =(-1,cosωx+
=(-1,cosωx+ sinωx),
sinωx), =(f(x),cosωx),其中ω>0,且
=(f(x),cosωx),其中ω>0,且 ,又f(x)的图象两相邻对称轴的距离为
,又f(x)的图象两相邻对称轴的距离为 .
.
(1)求ω的值;
(2)求函数f(x)在[0,2π]上的单调递减区间.
解:(1)由题意 =0,
=0,
∴f(x)=cosωx(cosωx+ sinωx)
sinωx)
=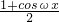 +
+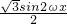
=
由题意,函数周期为3π,又ω>0,∴ω= ;
;
(2)由(1)知f(x)= ,
,
由
可得 ,
,
又x∈[0,2π],
∴f(x)的减区间是[ ,2π].
,2π].
分析:(1)由向量垂直可得数量积为0,代入可得函数解析式,由题意可得周期,进而可得ω的值;
(2)先由 解得总的单调区间,结合x∈[0,2π],可得答案.
解得总的单调区间,结合x∈[0,2π],可得答案.
点评:本题考查复合三角函数的单调性,涉及向量的数量积的运算,属中档题.
 =0,
=0,∴f(x)=cosωx(cosωx+
 sinωx)
sinωx)=
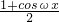 +
+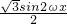
=

由题意,函数周期为3π,又ω>0,∴ω=
 ;
;(2)由(1)知f(x)=
 ,
,由

可得
 ,
,又x∈[0,2π],
∴f(x)的减区间是[
 ,2π].
,2π].分析:(1)由向量垂直可得数量积为0,代入可得函数解析式,由题意可得周期,进而可得ω的值;
(2)先由
 解得总的单调区间,结合x∈[0,2π],可得答案.
解得总的单调区间,结合x∈[0,2π],可得答案.点评:本题考查复合三角函数的单调性,涉及向量的数量积的运算,属中档题.

练习册系列答案
相关题目