题目内容
设p:实数m满足m2-4am+3a2<0(其中a<0);q:实数m满足方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线.若?p是?q的必要不充分条件,求实数a的取值范围.
设A={m|m2-4am+3a2<0,a<0}={m|3a<m<a,a<0},
因为方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线,
即
-
=1为双曲线,
所以(m+4)(m+2)<0,…(4分)
设B={m|(m+4)(m+2)>0}={m|m<-4,或m>-2}
因为?p是?q的必要不充分条件,所以q是p的必要不充分条件.…(6分)
所以{m|3a<m<a,a<0}?{m|m<-4,或m>-2}…(8分)
则
或
,…(10分)
解得:-
≤a<0或a≤-4
故实数的取值范围为{a|-
≤a<0或a≤-4}…(12分)
因为方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线,
即
| x2 |
| m+2 |
| y2 |
| m+4 |
所以(m+4)(m+2)<0,…(4分)
设B={m|(m+4)(m+2)>0}={m|m<-4,或m>-2}
因为?p是?q的必要不充分条件,所以q是p的必要不充分条件.…(6分)
所以{m|3a<m<a,a<0}?{m|m<-4,或m>-2}…(8分)
则
|
|
解得:-
| 2 |
| 3 |
故实数的取值范围为{a|-
| 2 |
| 3 |

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
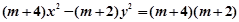 为双曲线,且
为双曲线,且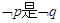 的必要不充分条件,求a的取值范围。
的必要不充分条件,求a的取值范围。