题目内容
已知f(x)=ae-x+cosx-x(0<x<1)
(1)若对任意的x∈(0,1),f(x)<0恒成立,求实数a的取值范围;
(2)求证:e-x+sinx<1+
(0<x<1).
(1)若对任意的x∈(0,1),f(x)<0恒成立,求实数a的取值范围;
(2)求证:e-x+sinx<1+
| x2 |
| 2 |
(1)由f(x)<0,得a<(x-cosx)•ex,
记g(x)=(x-cosx)•ex,
则g′(x)=(1+sinx)•ex+(x-cosx)•ex
=(1+sinx-cosx+x)•ex,
∵0<x<1,
∴sinx>0,1-cosx>0,ex>0,∴g′(x)>0,
∴g(x)在(0,1)上为增函数.
∴-1<g(x)<(1-cos1)•e,故a≤-1.
(2)构造函数h(x)=e-x+sinx-1-
(0<x<1),且h(0)=0,
则h′(x)=-e-x+cosx-x,
由(1)知:当a=-1时,f(x)=-e-x+cosx-x<0(0<x<1),
∴h(x)在(0,1)单调递减,∴h(x)<h(0)=0,
即e-x+sinx<1+
(0<x<1).
记g(x)=(x-cosx)•ex,
则g′(x)=(1+sinx)•ex+(x-cosx)•ex
=(1+sinx-cosx+x)•ex,
∵0<x<1,
∴sinx>0,1-cosx>0,ex>0,∴g′(x)>0,
∴g(x)在(0,1)上为增函数.
∴-1<g(x)<(1-cos1)•e,故a≤-1.
(2)构造函数h(x)=e-x+sinx-1-
| x2 |
| 2 |
则h′(x)=-e-x+cosx-x,
由(1)知:当a=-1时,f(x)=-e-x+cosx-x<0(0<x<1),
∴h(x)在(0,1)单调递减,∴h(x)<h(0)=0,
即e-x+sinx<1+
| x2 |
| 2 |

练习册系列答案
相关题目
 .
.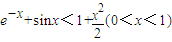 .
. .
.