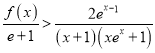Question

【题目】选修4-5：不等式选讲

已知函数

(Ⅰ)已知常数解关于的不等式；

（Ⅱ）若函数的图象恒在函数图象的上方，求实数的取值范围.

Answer 1

【答案】（Ⅰ）（Ⅱ）

【解析】试题分析: （Ⅰ）去掉绝对值结合即可求出不等式的解集;（Ⅱ）函数的图像恒在函数图像的上方，转化为恒成立,分离参变量,利用绝对值不等式求出函数的最值,进而求得参数的范围.

试题解析:（Ⅰ）由得,所以或

所以或,故不等式解集为

（Ⅱ）因为函数的图像恒在函数图像的上方，所以恒成立，则恒成立，因为,所以的取值范围是

点睛:本题考查解不等式以及由恒成立问题转化的含绝对值函数的最值问题,属于基础题目. 对绝对值三角不等式:|a|－|b|≤|a±b|≤|a|＋|b|.(1)当ab≥0时，|a＋b|＝|a|＋|b|；当ab≤0时，|a－b|＝|a|＋|b|.(2)该定理可以推广为|a＋b＋c|≤|a|＋|b|＋|c|，也可强化为||a|－|b||≤|a±b|≤|a|＋|b|，它们经常用于含绝对值的不等式的推证．