题目内容
在△ABC中角A、B、C所对的边是a、b、c，且a=2bsinA，则角B=
- A.30°
- B.60°
- C.30°或150°
- D.60°或120°
C
分析：利用正弦定理对已知条件化简可求sinB，结合三角形的内角范围可求B
解答：∵a=2bsinA，
由正弦定理可得sinA=2sinBsinA
∵0＜sinA＜1
∴
，
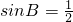∵0°＜B＜180°
∴B=30°或150°
故选C．
点评：本题以三角形为载体，考查正弦定理的运用，考查特殊角的三角函数，属于基础题．
分析：利用正弦定理对已知条件化简可求sinB，结合三角形的内角范围可求B
解答：∵a=2bsinA，
由正弦定理可得sinA=2sinBsinA
∵0＜sinA＜1
∴
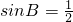，∵0°＜B＜180°
∴B=30°或150°
故选C．
点评：本题以三角形为载体，考查正弦定理的运用，考查特殊角的三角函数，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目