题目内容
设数列{an}满足a1=2,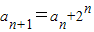 (n∈N*).
(n∈N*).(1)求数列{an}的通项公式;
(2)去掉数列{an}中的第3项,第6项,第9项,…,第3n项…,余下的项按顺序不变,重新组成一个新数列{bn},求{bn}的前n项和Tn.
【答案】分析:(1)a1=2,因为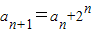 所以
所以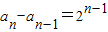
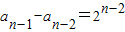 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.
(2)当n=2k时,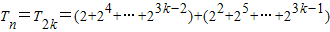 =
=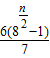 ;当n=2k+1时,
;当n=2k+1时,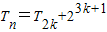 =
=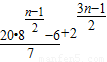 ,由此能求出Tn.
,由此能求出Tn.
解答:解:(1)a1=2,
因为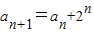
所以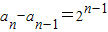
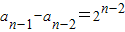
…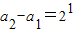
将上述等式两边分别相加,
得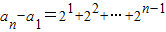 =
=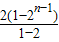 ,
,
所以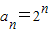 .…(6分)
.…(6分)
(2)当n=2k时,
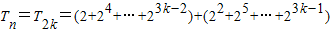
=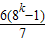 …(10分)
…(10分)
=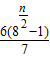 ;
;
当n=2k+1时,
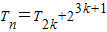
=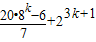
=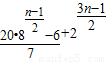 .…(14分)
.…(14分)
综上可得Tn=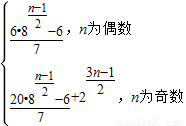 .…(16分)
.…(16分)
点评:本题考查数列的通项公式和数列的前n项和的求法,解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的合理运用.
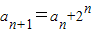 所以
所以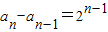
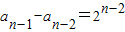 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.(2)当n=2k时,
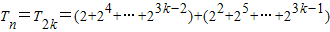 =
=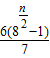 ;当n=2k+1时,
;当n=2k+1时,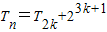 =
=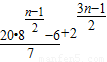 ,由此能求出Tn.
,由此能求出Tn.解答:解:(1)a1=2,
因为
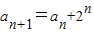
所以
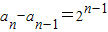
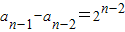
…
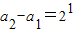
将上述等式两边分别相加,
得
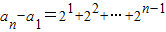 =
=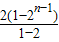 ,
,所以
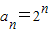 .…(6分)
.…(6分)(2)当n=2k时,
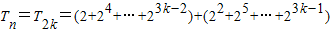
=
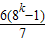 …(10分)
…(10分)=
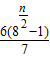 ;
;当n=2k+1时,
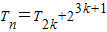
=
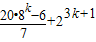
=
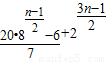 .…(14分)
.…(14分)综上可得Tn=
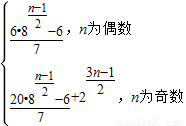 .…(16分)
.…(16分)点评:本题考查数列的通项公式和数列的前n项和的求法,解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|