题目内容
设数列{an}的前n项和为Sn,已知a1=1,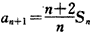 (n=1,2,3,…),
(n=1,2,3,…),
证明:(1)数列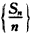 是等比数列;
是等比数列;
(2)Sn+1=4an.
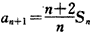 (n=1,2,3,…),
(n=1,2,3,…),证明:(1)数列
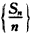 是等比数列;
是等比数列; (2)Sn+1=4an.
证明:(1)∵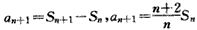 ,
,
∴(n+2)Sn=n(Sn+1-Sn),
整理,得nSn+1=2(n+1)Sn,
∴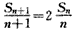 ,
,
故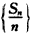 是以1为首项,2为公比的等比数列.
是以1为首项,2为公比的等比数列.
(2)由(1)知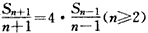 ,
,
于是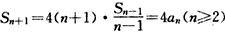 ,
,
又a2=3S1=3,
故S2=a1+a2=4=4a1,
因此,对于任意的正整数n≥1,都有Sn+1=4an。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目