题目内容
设首项为1的正项数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且Tn=
,其中p为常数.
(1)求p的值;
(2)求证:数列{an}为等比数列;
(3)证明:“数列an,2xan+1,2yan+2成等差数列,其中x、y均为整数”的充要条件是“x=1,且y=2”.
| 4-(Sn-p)2 | 3 |
(1)求p的值;
(2)求证:数列{an}为等比数列;
(3)证明:“数列an,2xan+1,2yan+2成等差数列,其中x、y均为整数”的充要条件是“x=1,且y=2”.
分析:(1)n=1时,由1=
求得p的值,再排除p=0的情形即可得到结论;
(2)当p=2时,Tn=
-
(2-Sn)2,再写一式,两式相减可得3an+1=4-Sn+1-Sn,再写一式,两式相减,可得数列{an}是等比数列;
(3)分充分性与必要性分别证明,必须搞清证明中的条件与结论.
| 4-(1-p)2 |
| 3 |
(2)当p=2时,Tn=
| 4 |
| 3 |
| 1 |
| 3 |
(3)分充分性与必要性分别证明,必须搞清证明中的条件与结论.
解答:(1)解:n=1时,由1=
得p=0或2,
若p=0时,Tn=
,
当n=2时,1+a22=
,解得a2=0或a2=-
,
而an>0,所以p=0不符合题意,故p=2;
(2)证明:当p=2时,Tn=
-
(2-Sn)2①,则Tn+1=
-
(2-Sn+1)2②,
②-①并化简得3an+1=4-Sn+1-Sn③,则3an+2=4-Sn+2-Sn+1④,
④-③得an+2=
an+1(n∈N*),
又因为a2=
a1,所以数列{an}是等比数列,且an=
;
(3)证明:充分性:若x=1,y=2,由an=
知an,2xan+1,2yan+2依次为
,
,
,
满足2×
=
+
,即an,2xan+1,2yan+2成等差数列;
必要性:假设an,2xan+1,2yan+2成等差数列,其中x、y均为整数,又an=
,
所以2•2x•
=
+2y•
,化简得2x-2y-2=1
显然x>y-2,设k=x-(y-2),
因为x、y均为整数,所以当k≥2时,2x-2y-2>1或2x-2y-2<1,
故当k=1,且当x=1,且y-2=0时上式成立,即证.
| 4-(1-p)2 |
| 3 |
若p=0时,Tn=
| 4-Sn2 |
| 3 |
当n=2时,1+a22=
| 4-(1+a2)2 |
| 3 |
| 1 |
| 2 |
而an>0,所以p=0不符合题意,故p=2;
(2)证明:当p=2时,Tn=
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
②-①并化简得3an+1=4-Sn+1-Sn③,则3an+2=4-Sn+2-Sn+1④,
④-③得an+2=
| 1 |
| 2 |
又因为a2=
| 1 |
| 2 |
| 1 |
| 2n-1 |
(3)证明:充分性:若x=1,y=2,由an=
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 2 |
| 2n |
| 4 |
| 2n+1 |
满足2×
| 2 |
| 2n |
| 1 |
| 2n-1 |
| 4 |
| 2n+1 |
必要性:假设an,2xan+1,2yan+2成等差数列,其中x、y均为整数,又an=
| 1 |
| 2n-1 |
所以2•2x•
| 1 |
| 2n |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
显然x>y-2,设k=x-(y-2),
因为x、y均为整数,所以当k≥2时,2x-2y-2>1或2x-2y-2<1,
故当k=1,且当x=1,且y-2=0时上式成立,即证.
点评:本题主要考查等差、等比数列的定义与通项公式、求和公式等基础知识,考查灵活运用基本量进行探索求解、推理分析能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
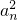 的前n项和为Tn,且
的前n项和为Tn,且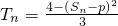 ,其中p为常数.
,其中p为常数.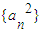 的前n项和为Tn,且
的前n项和为Tn,且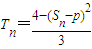 ,其中p为常数.
,其中p为常数.