题目内容
双曲线x2-y2=2的左、右焦点分别为F1、F2,点Pn(xn,yn)(n=1,2,3…)在其右支上,且满足|Pn+1F2|=|PnF1|,P1F2⊥F1F2,则x2010的值是
- A.4020

- B.4019

- C.4020
- D.4019
C
分析:由题意,知e= ,|PnF1|=|
,|PnF1|=| +|
+|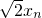 |=
|= +
+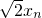 ,|Pn+1F2|=|
,|Pn+1F2|=| -
- |=
|= -
- ,xn+1=xn+2,又P1F2⊥F1F2,由此能求出x2010.
,xn+1=xn+2,又P1F2⊥F1F2,由此能求出x2010.
解答:依题意,e= ,
,
|PnF1|=| +|
+|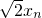 |=
|= +
+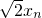 ,
,
|Pn+1F2|=| -
- |=
|= -
- ,
,
因为|Pn+1F2|=|PnF1|,所以xn+1=xn+2,又P1F2⊥F1F2,
所以x1=2,xn=2n,x2010=4020.
故选C.
点评:本题考查双曲线的基本性质和应用,解题时要注意公式的灵活运用.
分析:由题意,知e=
 ,|PnF1|=|
,|PnF1|=| +|
+|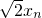 |=
|= +
+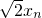 ,|Pn+1F2|=|
,|Pn+1F2|=| -
- |=
|= -
- ,xn+1=xn+2,又P1F2⊥F1F2,由此能求出x2010.
,xn+1=xn+2,又P1F2⊥F1F2,由此能求出x2010.解答:依题意,e=
 ,
,|PnF1|=|
 +|
+|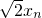 |=
|= +
+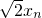 ,
,|Pn+1F2|=|
 -
- |=
|= -
- ,
,因为|Pn+1F2|=|PnF1|,所以xn+1=xn+2,又P1F2⊥F1F2,
所以x1=2,xn=2n,x2010=4020.
故选C.
点评:本题考查双曲线的基本性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目