题目内容
某单位为了参加上级组织的普及消防知识竞赛,需要从两名选手中选出一人参加.为此,设计了一个挑选方案:选手从6道备选题中一次性随机抽取3题.通过考察得知:6道备选题中选手甲有4道题能够答对,2道题答错;选手乙答对每题的概率都是
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
(1)写出ξ的概率分布列(不要求计算过程),并求出Eξ,Eη;
(2)求Dξ,Dη.请你根据得到的数据,建议该单位派哪个选手参加竞赛?
| 2 | 3 |
(1)写出ξ的概率分布列(不要求计算过程),并求出Eξ,Eη;
(2)求Dξ,Dη.请你根据得到的数据,建议该单位派哪个选手参加竞赛?
分析:(1)根据题意写出变量的可能取值,结合变量对应的事件写出写出变量对应的概率,写出变量的分布列,根据变量η服从二项分布,得到分布列,写出期望.
(2)根据第一问写出的两个变量的分布列,利用方差的公式写出变量的方差,由η~B(3,
),直接写出变量的方差,两个期望和方差进行比较得到结论.
(2)根据第一问写出的两个变量的分布列,利用方差的公式写出变量的方差,由η~B(3,
| 2 |
| 3 |
解答:解:(1)ξ的取值可能为1,2,3
P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
ξ的分布列是

∴Eξ=1×
+2×
+3×
=2
由题意知η~B(3,
)
∴Eη=3×
=2
(2)Dξ=(1-2)2×
+(2-2)2×
+(3-2)2×
=
∵η~B(3,
)
∴Dη=3×
×
=
从计算的结果来看,两个人的平均成绩相等,甲的方差比乙的方差小,
建议派甲参加竞赛.
P(ξ=1)=
| ||||
|
| 1 |
| 5 |
| ||||
|
| 3 |
| 5 |
| ||||
|
| 1 |
| 5 |
ξ的分布列是

∴Eξ=1×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
由题意知η~B(3,
| 2 |
| 3 |
∴Eη=3×
| 2 |
| 3 |
(2)Dξ=(1-2)2×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
∵η~B(3,
| 2 |
| 3 |
∴Dη=3×
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
从计算的结果来看,两个人的平均成绩相等,甲的方差比乙的方差小,
建议派甲参加竞赛.
点评:本题考查离散型随机变量的分布列和期望,考查变量的方差,利用方差和期望的意义,考查它们的实际应用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
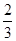 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η. ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η. ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η. ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.