题目内容
正三棱柱ABC-A1B1C1内接于半径为1的球,则当该棱柱体积最大时,高h=( )A.

B.

C.

D.

【答案】分析:由正三棱柱ABC-A1B1C1内接于半径为1的球,该棱柱的高为h,则球心到正三棱柱底面ABC的距离d= h,进而根据底面半径r,球心距d,球半径R构成直角三角形,满足勾股定理,可得底面半径r,再由等边三角形外接圆半径与边长的关系,可得底面边长a,进而得到底面面积,和棱柱的体积,利用导数法可得该棱柱体积最大时,高h的值.
h,进而根据底面半径r,球心距d,球半径R构成直角三角形,满足勾股定理,可得底面半径r,再由等边三角形外接圆半径与边长的关系,可得底面边长a,进而得到底面面积,和棱柱的体积,利用导数法可得该棱柱体积最大时,高h的值.
解答:解:设该棱柱的高为h,
由正三棱柱ABC-A1B1C1内接于半径为1的球,
可得球心到正三棱柱底面ABC的距离d= h
h
则正三棱柱底面ABC的底面半径r=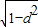 =
=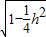
则正三棱柱底面ABC的底面边长a=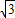 r=
r=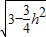
则正三棱柱底面ABC的底面面积S=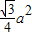 =
=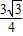 -
-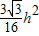
则正三棱柱ABC-A1B1C1的体积V= Sh=
Sh=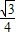 h-
h-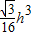
则V′=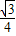 -
-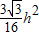
令V′=0,则h=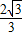
故当该棱柱体积最大时,高h=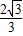
故选D
点评:本题考查的知识点是球内接多面体,解答本题的关键是熟练掌握底面半径r,球心距d,球半径R构成直角三角形,满足勾股定理,及正三角形边长,面积,外接圆半径之间的关系.
 h,进而根据底面半径r,球心距d,球半径R构成直角三角形,满足勾股定理,可得底面半径r,再由等边三角形外接圆半径与边长的关系,可得底面边长a,进而得到底面面积,和棱柱的体积,利用导数法可得该棱柱体积最大时,高h的值.
h,进而根据底面半径r,球心距d,球半径R构成直角三角形,满足勾股定理,可得底面半径r,再由等边三角形外接圆半径与边长的关系,可得底面边长a,进而得到底面面积,和棱柱的体积,利用导数法可得该棱柱体积最大时,高h的值.解答:解:设该棱柱的高为h,
由正三棱柱ABC-A1B1C1内接于半径为1的球,
可得球心到正三棱柱底面ABC的距离d=
 h
h则正三棱柱底面ABC的底面半径r=
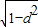 =
=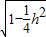
则正三棱柱底面ABC的底面边长a=
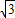 r=
r=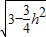
则正三棱柱底面ABC的底面面积S=
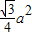 =
=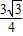 -
-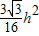
则正三棱柱ABC-A1B1C1的体积V=
 Sh=
Sh=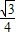 h-
h-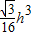
则V′=
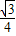 -
-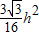
令V′=0,则h=
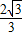
故当该棱柱体积最大时,高h=
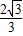
故选D
点评:本题考查的知识点是球内接多面体,解答本题的关键是熟练掌握底面半径r,球心距d,球半径R构成直角三角形,满足勾股定理,及正三角形边长,面积,外接圆半径之间的关系.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.