题目内容
(1)判断函数f(x)= 在x∈(0,+∞)上的单调性并证明你的结论?
在x∈(0,+∞)上的单调性并证明你的结论?
(2)猜想函数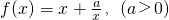 在x∈(-∞,0)∪(0,+∞)上的单调性?(只需写出结论,不用证明)
在x∈(-∞,0)∪(0,+∞)上的单调性?(只需写出结论,不用证明)
(3)利用题(2)的结论,求使不等式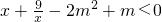 在x∈[1,5]上恒成立时的实数m的取值范围?
在x∈[1,5]上恒成立时的实数m的取值范围?
(1)解:函数f(x)= 在(0,2]上是减函数,在[2,+∞)上是增函数.…(1分)
在(0,2]上是减函数,在[2,+∞)上是增函数.…(1分)
证明:设任意x1<x2∈(0,+∞),则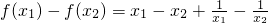 …(2分)
…(2分)
=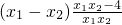 …(3分)
…(3分)
又设x1<x2∈(0,2],则f(x1)-f(x2)>0,∴f(x1)>f(x2)
∴函数f(x)= 在(0,2]上是减函数 …(4分)
在(0,2]上是减函数 …(4分)
又设x1<x2∈[2,+∞),则f(x1)-f(x2)<0,∴f(x1)<f(x2)
∴函数f(x)= 在[2,+∞)上是增函数 …(5分)
在[2,+∞)上是增函数 …(5分)
(2)解:由上及f(x)是奇函数,可猜想:f(x)在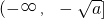 和
和 上是增函数,f(x)在
上是增函数,f(x)在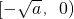 和
和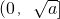 上是减函数 …(7分)
上是减函数 …(7分)
(3)解:∵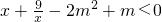 在x∈[1,5]上恒成立
在x∈[1,5]上恒成立
∴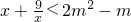 在x∈[1,5]上恒成立 …(8分)
在x∈[1,5]上恒成立 …(8分)
由(2)中结论,可知函数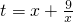 在x∈[1,5]上的最大值为10,
在x∈[1,5]上的最大值为10,
此时x=1 …(10分)
要使原命题成立,当且仅当2m2-m>10
∴2m2-m-10>0 解得m<-2,或
∴实数m的取值范围是{m|m<-2,或 } …(12分)
} …(12分)
分析:(1)函数f(x)= 在(0,2]上是减函数,在[2,+∞)上是增函数,再利用单调性的定义进行证明即可;
在(0,2]上是减函数,在[2,+∞)上是增函数,再利用单调性的定义进行证明即可;
(2)由上及f(x)是奇函数,可猜想:f(x)在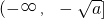 和
和 上是增函数,f(x)在
上是增函数,f(x)在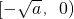 和
和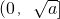 上是减函数
上是减函数
(3)根据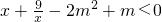 在x∈[1,5]上恒成立,可得
在x∈[1,5]上恒成立,可得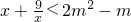 在x∈[1,5]上恒成立 求出左边函数的最小值即可.
在x∈[1,5]上恒成立 求出左边函数的最小值即可.
点评:本题重点考查函数的单调性的判定与证明,考查恒成立问题,解题的关键是利用单调性的定义,利用函数的最值解决恒成立问题.
 在(0,2]上是减函数,在[2,+∞)上是增函数.…(1分)
在(0,2]上是减函数,在[2,+∞)上是增函数.…(1分)证明:设任意x1<x2∈(0,+∞),则
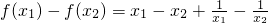 …(2分)
…(2分)=
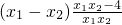 …(3分)
…(3分)又设x1<x2∈(0,2],则f(x1)-f(x2)>0,∴f(x1)>f(x2)
∴函数f(x)=
 在(0,2]上是减函数 …(4分)
在(0,2]上是减函数 …(4分)又设x1<x2∈[2,+∞),则f(x1)-f(x2)<0,∴f(x1)<f(x2)
∴函数f(x)=
 在[2,+∞)上是增函数 …(5分)
在[2,+∞)上是增函数 …(5分)(2)解:由上及f(x)是奇函数,可猜想:f(x)在
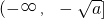 和
和 上是增函数,f(x)在
上是增函数,f(x)在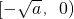 和
和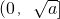 上是减函数 …(7分)
上是减函数 …(7分)(3)解:∵
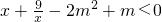 在x∈[1,5]上恒成立
在x∈[1,5]上恒成立∴
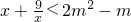 在x∈[1,5]上恒成立 …(8分)
在x∈[1,5]上恒成立 …(8分)由(2)中结论,可知函数
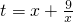 在x∈[1,5]上的最大值为10,
在x∈[1,5]上的最大值为10,此时x=1 …(10分)
要使原命题成立,当且仅当2m2-m>10
∴2m2-m-10>0 解得m<-2,或

∴实数m的取值范围是{m|m<-2,或
 } …(12分)
} …(12分)分析:(1)函数f(x)=
 在(0,2]上是减函数,在[2,+∞)上是增函数,再利用单调性的定义进行证明即可;
在(0,2]上是减函数,在[2,+∞)上是增函数,再利用单调性的定义进行证明即可;(2)由上及f(x)是奇函数,可猜想:f(x)在
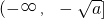 和
和 上是增函数,f(x)在
上是增函数,f(x)在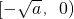 和
和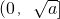 上是减函数
上是减函数 (3)根据
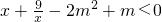 在x∈[1,5]上恒成立,可得
在x∈[1,5]上恒成立,可得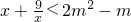 在x∈[1,5]上恒成立 求出左边函数的最小值即可.
在x∈[1,5]上恒成立 求出左边函数的最小值即可.点评:本题重点考查函数的单调性的判定与证明,考查恒成立问题,解题的关键是利用单调性的定义,利用函数的最值解决恒成立问题.

练习册系列答案
相关题目