题目内容
对于正实数a,函数y=x+| a |
| x |
| 3 |
| 4 |
分析:利用证明单调性的定义法得到关于参数的不等式,化简成不等式恒成立的情况,求出参数的取值范围,再根据参数的取值范围判断函数的单调区间.
解答:解:∵y=x+
在(
,+∞)上为增函数.
∴
<x1<x2时y1<y2,
即x1+
-x2-
=
<0?x1x2-a>0?a<x1x2在
<x1<x2时恒成立,∴a≤
,
f(x)=loga(3x2-4x)的定义域为
(-∞,0)∪(
,+∞),而0<a≤
<1,
∴f(x)与g(x)=3x2-4x在(-∞,0),(
,+∞)上的单调性相反,
∴f(x)的单调递减区间为(
,+∞).
答:f(x)的单调递减区间为(
,+∞).
| a |
| x |
| 3 |
| 4 |
∴
| 3 |
| 4 |
即x1+
| a |
| x1 |
| a |
| x2 |
| (x1-x2)(x1x2-a) |
| x1x2 |
| 3 |
| 4 |
| 9 |
| 16 |
f(x)=loga(3x2-4x)的定义域为
(-∞,0)∪(
| 3 |
| 4 |
| 9 |
| 16 |
∴f(x)与g(x)=3x2-4x在(-∞,0),(
| 4 |
| 3 |
∴f(x)的单调递减区间为(
| 4 |
| 3 |
答:f(x)的单调递减区间为(
| 4 |
| 3 |
点评:本考点考查函数的单调性,由单调性求参数,以及求复合函数的单调区间,解本题判断出参数的取值范围是关键.

练习册系列答案
相关题目
 在(
在( ,+∞)上为增函数,求函数f(x)=loga(3x2-4x)的单调递减区间.
,+∞)上为增函数,求函数f(x)=loga(3x2-4x)的单调递减区间.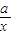 在(
在( ,+∞)上为增函数,求函数f(x)=loga(3x2-4x)的单调递减区间.
,+∞)上为增函数,求函数f(x)=loga(3x2-4x)的单调递减区间. 在(
在( ,+∞)上为增函数,求函数f(x)=loga(3x2-4x)的单调递减区间.
,+∞)上为增函数,求函数f(x)=loga(3x2-4x)的单调递减区间.