题目内容
设函数 ,集合A={x|y=f(x)},B={y|y=f(x)},则A∪B=________.
,集合A={x|y=f(x)},B={y|y=f(x)},则A∪B=________.
[-5,4]
分析:根据题意,对于函数 ,令t=-x2-2x+15,由二次函数的性质,可得f(x)的定义域与值域,分析可得集合A为f(x)的定义域,B为函数f(x)的值域,即可得集合A、B,由并集的定义,计算可得答案.
,令t=-x2-2x+15,由二次函数的性质,可得f(x)的定义域与值域,分析可得集合A为f(x)的定义域,B为函数f(x)的值域,即可得集合A、B,由并集的定义,计算可得答案.
解答:根据题意,对于函数 ,
,
令t=-x2-2x+15,
必有t=-x2-2x+15≥0,解可得-5≤x≤3,即f(x)的定义域为[-5,3],
分析可得0≤t≤16,则有0≤f(x)≤4,即f(x)的值域为[0,4],
集合A为f(x)的定义域,B为函数f(x)的值域,
则A=[-5,3],B=[0,4],
则A∪B=[-5,4];
故答案为[-5,4].
点评:本题考查函数的定义域、值域的计算与交集的求法,关键是认清集合A、B.
分析:根据题意,对于函数
 ,令t=-x2-2x+15,由二次函数的性质,可得f(x)的定义域与值域,分析可得集合A为f(x)的定义域,B为函数f(x)的值域,即可得集合A、B,由并集的定义,计算可得答案.
,令t=-x2-2x+15,由二次函数的性质,可得f(x)的定义域与值域,分析可得集合A为f(x)的定义域,B为函数f(x)的值域,即可得集合A、B,由并集的定义,计算可得答案.解答:根据题意,对于函数
 ,
,令t=-x2-2x+15,
必有t=-x2-2x+15≥0,解可得-5≤x≤3,即f(x)的定义域为[-5,3],
分析可得0≤t≤16,则有0≤f(x)≤4,即f(x)的值域为[0,4],
集合A为f(x)的定义域,B为函数f(x)的值域,
则A=[-5,3],B=[0,4],
则A∪B=[-5,4];
故答案为[-5,4].
点评:本题考查函数的定义域、值域的计算与交集的求法,关键是认清集合A、B.

练习册系列答案
相关题目
 ,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )
,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( ) ,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )
,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( ) ,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )
,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )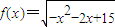 ,集合A={x|y=f(x)},B={y|y=f(x)},则右图中阴影部分表示的集合为( )
,集合A={x|y=f(x)},B={y|y=f(x)},则右图中阴影部分表示的集合为( )