题目内容
已知点P是圆x2+y2=1上任意一点,过点P作y轴的垂线,垂足为Q,点R满足 ,记点R的轨迹为曲线C.
,记点R的轨迹为曲线C.(Ⅰ)求曲线C的方程;
(Ⅱ)设A(0,1),点M、N在曲线C上,且直线AM与直线AN的斜率之积为
 ,求△AMN的面积的最大值.
,求△AMN的面积的最大值.
【答案】分析:(I)根据 ,确定P,R坐标之间的关系,利用点P是圆x2+y2=1上任意一点,可得点R的轨迹方程;
,确定P,R坐标之间的关系,利用点P是圆x2+y2=1上任意一点,可得点R的轨迹方程;
(Ⅱ)(1)当直线MN的斜率不存在时,不合题意;
(2)当直线MN的斜率存在时,确定直线MN过定点T(0,-3),再计算△AMN的面积,利用换元法,借助于基本不等式,即可求得△AMN的面积的最大值.
解答:解:(I)设R(x,y),P(x,y),则Q(0,y).
∵ ,∴
,∴ ,
,
∵点P是圆x2+y2=1上任意一点,
∴ ,
,
∴点R的轨迹方程: .…(6分)
.…(6分)
(Ⅱ)(1)当直线MN的斜率不存在时,设MN: .
.
则 ,
, ,∴
,∴ ,不合题意.…(7分)
,不合题意.…(7分)
(2)当直线MN的斜率存在时,设lMN:y=kx+b,M(x1,y1),N(x2,y2)
联立方程 ,得(1+3k2)x2+6kbx+3b2-3=0.
,得(1+3k2)x2+6kbx+3b2-3=0.
∴△=12(3k2-b2+1)>0, ,
, .…(9分)
.…(9分)
又 ,
,
即 .
.
将 ,
, 代入上式,得b=-3.
代入上式,得b=-3.
∴直线MN过定点T(0,-3).…(11分)
∴ =
= .…(13分)
.…(13分)
令 ,即3k2=t2+8,∴
,即3k2=t2+8,∴ .
.
当且仅当t=3时, .…(15分)
.…(15分)
点评:本题考查轨迹方程的求解,考查三角形的面积,解题的关键是利用代入法求轨迹方程,构建面积函数,利用基本不等式求最值.
 ,确定P,R坐标之间的关系,利用点P是圆x2+y2=1上任意一点,可得点R的轨迹方程;
,确定P,R坐标之间的关系,利用点P是圆x2+y2=1上任意一点,可得点R的轨迹方程;(Ⅱ)(1)当直线MN的斜率不存在时,不合题意;
(2)当直线MN的斜率存在时,确定直线MN过定点T(0,-3),再计算△AMN的面积,利用换元法,借助于基本不等式,即可求得△AMN的面积的最大值.
解答:解:(I)设R(x,y),P(x,y),则Q(0,y).
∵
 ,∴
,∴ ,
,∵点P是圆x2+y2=1上任意一点,
∴
 ,
,∴点R的轨迹方程:
 .…(6分)
.…(6分)(Ⅱ)(1)当直线MN的斜率不存在时,设MN:
 .
.则
 ,
, ,∴
,∴ ,不合题意.…(7分)
,不合题意.…(7分)(2)当直线MN的斜率存在时,设lMN:y=kx+b,M(x1,y1),N(x2,y2)
联立方程
 ,得(1+3k2)x2+6kbx+3b2-3=0.
,得(1+3k2)x2+6kbx+3b2-3=0.∴△=12(3k2-b2+1)>0,
 ,
, .…(9分)
.…(9分)又
 ,
,即
 .
.将
 ,
, 代入上式,得b=-3.
代入上式,得b=-3.∴直线MN过定点T(0,-3).…(11分)
∴
 =
= .…(13分)
.…(13分)令
 ,即3k2=t2+8,∴
,即3k2=t2+8,∴ .
.当且仅当t=3时,
 .…(15分)
.…(15分)点评:本题考查轨迹方程的求解,考查三角形的面积,解题的关键是利用代入法求轨迹方程,构建面积函数,利用基本不等式求最值.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
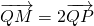 的点M的轨迹为曲线C.
的点M的轨迹为曲线C. 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.