题目内容
若过原点的直线l与连接P(2，2)，Q(6，2
)的线段相交，则直线l倾斜角范围
| 3 |
[
，
]
| π |
| 6 |
| π |
| 4 |
[
，
]
．| π |
| 6 |
| π |
| 4 |
分析：由斜率公式可得直线OP，OQ的斜率，数形结合可得当直线l过原点且介于OP，OQ之间满足题意，可得直线斜率的范围，由斜率和倾斜角的关系可得角的范围．
解答：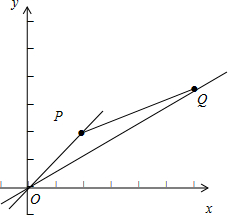
解：由斜率公式可得kOP=
=1，kOQ=
=
，
如图可知，当直线l过原点且介于OP，OQ之间满足题意，
故直线l的斜率k满足
≤k≤1，
故直线l的倾斜角α满足
≤tanα≤1，
结合倾斜角的范围可得
≤α≤
故直线l倾斜角范围为：[
，
]
故答案为：[
，
]
解：由斜率公式可得kOP=| 2-0 |
| 2-0 |
2
| ||
| 6-0 |
| ||
| 3 |
如图可知，当直线l过原点且介于OP，OQ之间满足题意，
故直线l的斜率k满足
| ||
| 3 |
故直线l的倾斜角α满足
| ||
| 3 |
结合倾斜角的范围可得
| π |
| 6 |
| π |
| 4 |
故直线l倾斜角范围为：[
| π |
| 6 |
| π |
| 4 |
故答案为：[
| π |
| 6 |
| π |
| 4 |
点评：本题考查直线的倾斜角和直线斜率的关系，数形结合是解决问题的关键，属基础题．
练习册系列答案
学业测评一课一测系列答案
相关题目
，l与x轴交于E，一条渐近线方程是y＝
x，线段PQ是过曲线C右焦点F的一条弦．
＝0，当P在曲线C上运动时，求a的取值范围；
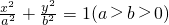上任一点P到两个焦点的距离的和为
，P与椭圆长轴两顶点连线的斜率之积为
．设直线l过椭圆C的右焦点F，交椭圆C于两点A（x1，y1），B（x2，y2）．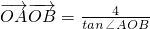
（O为坐标原点），求|y1-y2|的值；