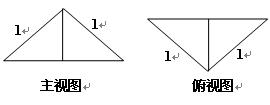
题目内容
如图,已知正方体 的棱长为2,E、F分别是
的棱长为2,E、F分别是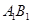 、
、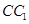 的中点,过
的中点,过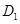 、E、F作平面
、E、F作平面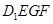 交
交 于G.
于G.
(l)求证:EG∥ ;
;
(2)求二面角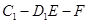 的余弦值;
的余弦值;
(3)求正方体被平面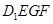 所截得的几何体
所截得的几何体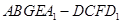 的体积.
的体积.
(1)详见试题解析(2)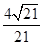 (3)
(3)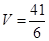
解析试题分析:(1)两平行平面都与第三个平面相交,则交线平行;
(2)以 为原点分别以
为原点分别以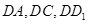 为
为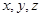 轴,建立空间直角坐标系,平面
轴,建立空间直角坐标系,平面 的法向量为
的法向量为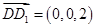 ,求出平面
,求出平面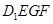 的法向量
的法向量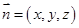
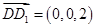 ,利用空间向量的夹角公式求二面角的余弦值.
,利用空间向量的夹角公式求二面角的余弦值.
(3)所求几何体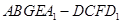 是由正方体
是由正方体 截去一个三棱台
截去一个三棱台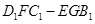 而得到, 所以,
而得到, 所以,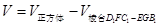 .
.
(1)证明:在正方体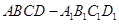 中,因为平面
中,因为平面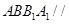 平面
平面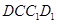 ,
,
平面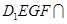 平面
平面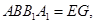 平面
平面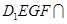 平面
平面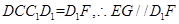
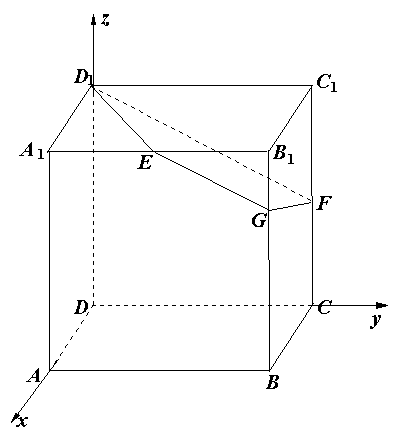
(2)解:如图,以 为原点分别以
为原点分别以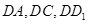 为
为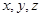 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则有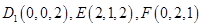
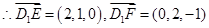
设平面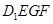 的法向量为
的法向量为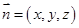 则由
则由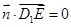 和
和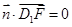 得
得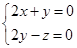
取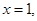 得
得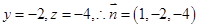
又平面 的法向量为
的法向量为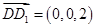
故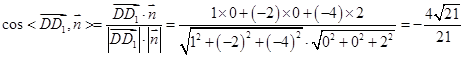
所以截面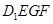 与底面
与底面 所成二面角的余弦值为
所成二面角的余弦值为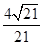
(3)解:设所截几何体 的体积为
的体积为
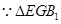 与
与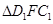 相似,
相似,
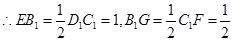
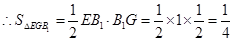
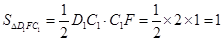
故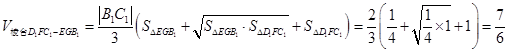

考点:1、平面与平面平行的性质;2、空间直角坐标系;3、向量夹角公式;4、组合体的体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
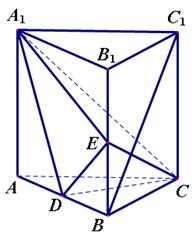
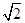 ,求三棱锥D一A1CE的体积.
,求三棱锥D一A1CE的体积. .
.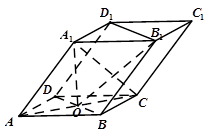
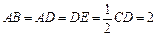 ,M是线段AE上的动点.
,M是线段AE上的动点.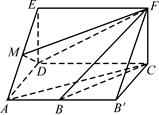
 是AC的中点,已知
是AC的中点,已知 ,
,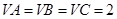 .
.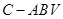 的体积.
的体积.
 中,已知
中,已知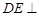 平面
平面 ,
,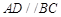 ,
,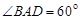 ,
,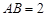 ,
,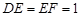 .
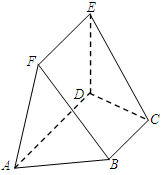
.
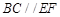 ;
;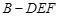 的体积.
的体积.
 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积. 图①
图① 图②
图②