题目内容
已知椭圆G与双曲线12x2-4y2=3有相同的焦点,且过点P(1,![]() ).
).
(1)求椭圆G的方程;
(2)设F1、F2是椭圆G的左焦点和右焦点,过F2的直线l:x=my+1与椭圆G相交于A、B两点,请问△ABF1的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
答案:
解析:
解析:
|
解:(1)双曲线 设椭圆的长轴长为 又 ∴椭圆G的方程 (2)如图,设
即 当 设 由 解得 ∴ 有 当 即当 ∴存在直线 |

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 ,得
,得 ,令
,令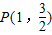 .
.