题目内容
已知函y=f（x）定义在[-
]上，且其导函数的图象如图所示，则函数y=f（x）可能是（ ）
A．y=sin
B．y=-sinx•cos
C．y=sinx•cos
D．y=cos
【答案】分析：先根据函数y=f（x）在[-
]上导函数的图象可知函数y=f（x）在[-
]上单调递增，且
与
是极值点，然后进行逐一进行判定即可．
解答：解：根据函数y=f（x）在[-
]上导函数的图象可知
函数y=f（x）在[-
]上单调递增，且
与
是极值点
选项A、在[-
]上单调递增，但
与
不是极值点，故不正确
选项B、在[-
]上单调递减，
与
是极值点，故不正确
选项C、在[-
]上单调递增，且
与
是极值点，故正确
选项D、在[-
]上不单调，故不正确
故选C．
点评：本题主要考查了函数的单调性与导数的关系，同时考查了识图能力，以及分类讨论的思想，属于基础题．
]上导函数的图象可知函数y=f（x）在[-]上单调递增，且与是极值点，然后进行逐一进行判定即可．解答：解：根据函数y=f（x）在[-
]上导函数的图象可知函数y=f（x）在[-
]上单调递增，且与是极值点选项A、在[-
]上单调递增，但与不是极值点，故不正确选项B、在[-
]上单调递减，与是极值点，故不正确选项C、在[-
]上单调递增，且与是极值点，故正确选项D、在[-
]上不单调，故不正确故选C．
点评：本题主要考查了函数的单调性与导数的关系，同时考查了识图能力，以及分类讨论的思想，属于基础题．
练习册系列答案
相关题目
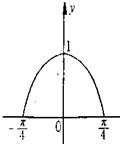已知函y=f（x）定义在[-| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=-sinx•cosx |
| C、y=sinx•cosx |
| D、y=cosx |
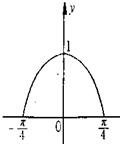已知函y=f（x）定义在[-
]上，且其导函数的图象如图所示，则函数y=f（x）可能是
]上，且其导函数的图象如图所示，则函数y=f（x）可能是（ ）
]上，且其导函数的图象如图所示，则函数y=f（x）可能是（ ）