题目内容
(本小题满分13分)
已知椭圆的中点在原点O,焦点在x轴上,点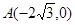 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且 ·
· ="0," |
="0," | |=|
|=| |.(点C在x轴上方)
|.(点C在x轴上方)
(I)求椭圆的方程;
(II)若平行于CO的直线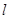 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求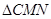 面积的最大值,并求此时直线
面积的最大值,并求此时直线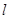 的方程.
的方程.
(I) ;(II)
;(II) ,
,
解析试题分析:(I)设椭圆的标准方程为


又∵C在椭圆上,
∴椭圆的标准方程为 …………5分
…………5分
(II)设
∵CO的斜率为-1,
∴设直线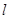 的方程为
的方程为
代入 刘
刘

又C到直线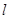 的距离
的距离
 的面积
的面积

当且仅当 时取等号,此时
时取等号,此时 满足题中条件,
满足题中条件,
∴直线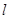 的方程为
的方程为 …………13分
…………13分
考点:椭圆的简单性质;椭圆的标准方程;直线与椭圆的综合应用。
点评:本题考查椭圆方程的求法和弦长的运算,解题时要注意椭圆性质的灵活运用和弦长公式的合理运用。在求直线与圆锥曲线相交的弦长时一般采用韦达定理设而不求的方法,在求解过程中一般采取步骤为:设点→联立方程→消元→韦达定理→弦长公式。

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
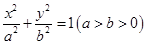 的离心率
的离心率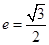 ,且短半轴
,且短半轴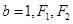 为其左右焦点,
为其左右焦点,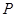 是椭圆上动点.
是椭圆上动点.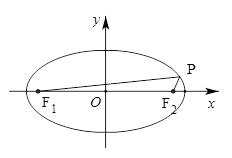
 时,求
时,求 面积;
面积;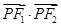 取值范围.
取值范围.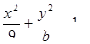 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点;  ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求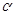 ,∠PF2F1=
,∠PF2F1=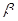 ,求cos
,求cos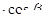 的值及
的值及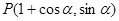 ,参数
,参数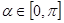 ,点Q在曲线C:
,点Q在曲线C: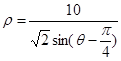 上.
上.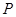 的轨迹方程和曲线C的方程;
的轨迹方程和曲线C的方程; 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在
在 轴上的截距为
轴上的截距为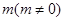 ,
, ,椭圆
,椭圆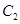 以
以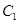 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线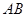 的方程.
的方程.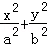 =1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足
=1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足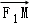
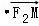 =0,点N( 0,3 )到椭圆上的点的最远距离为5
=0,点N( 0,3 )到椭圆上的点的最远距离为5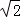
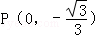 ;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由. 的离心率为
的离心率为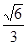 ,
, 为椭圆的右焦点,
为椭圆的右焦点,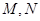 两点在椭圆
两点在椭圆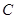 上,且
上,且 ,定点
,定点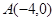 。
。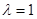 时,有
时,有 ,求椭圆
,求椭圆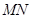 斜率为k,且设
斜率为k,且设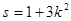 时,试求
时,试求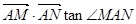 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时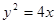 及点
及点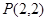 ,直线
,直线 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。 轴上截距的取值范围;
轴上截距的取值范围;