题目内容
16.已知x,y满足方程x2-y-1=0,当x>$\sqrt{3}$时,则m=$\frac{3x+y-5}{x-1}+\frac{x+3y-7}{y-2}$的最小值为8.分析 化简m=$\frac{3x+y-5}{x-1}+\frac{x+3y-7}{y-2}$=$\frac{y-2}{x-1}$+$\frac{x-1}{y-2}$+6,作函数y=x2-1,并作出点(1,2);$\frac{y-2}{x-1}$的几何意义是函数y=x2-1的点与点(1,2)的连线所成直线的斜率;从而可得$\frac{y-2}{x-1}$>0,从而由基本不等式求最小值即可.
解答 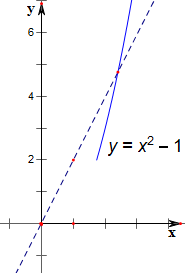 解:m=$\frac{3x+y-5}{x-1}+\frac{x+3y-7}{y-2}$
解:m=$\frac{3x+y-5}{x-1}+\frac{x+3y-7}{y-2}$
=3+$\frac{y-2}{x-1}$+3+$\frac{x-1}{y-2}$
=$\frac{y-2}{x-1}$+$\frac{x-1}{y-2}$+6,
由x2-y-1=0得y=x2-1,
作函数y=x2-1,并作出点(1,2);
$\frac{y-2}{x-1}$的几何意义是函数y=x2-1的点与点(1,2)的连线所成直线的斜率;
结合图象可得,
$\frac{y-2}{x-1}$>$\frac{3-1-2}{\sqrt{3}-1}$=0;
故$\frac{y-2}{x-1}$+$\frac{x-1}{y-2}$+6
≥2$\sqrt{\frac{y-2}{x-1}•\frac{x-1}{y-2}}$+6=8;
(当且仅当$\frac{y-2}{x-1}$=$\frac{x-1}{y-2}$时,等号成立);
故答案为:8.
点评 本题考查了函数的化简及学生作图的能力,同时考查了基本不等式的应用,属于难题.

练习册系列答案
相关题目
7.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±x,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{2}$ |
4.若函数y=f(x)在区间[a,b]上的图象是连续的,则下列说法正确的是( )
| A. | 若f(a)f(b)>0,则不存在实数c∈(a,b)使得f(c)=0 | |
| B. | 若f(a)f(b)>0,则有可能存在实数c∈(a,b)使得f(c)=0 | |
| C. | 若f(a)f(b)<0,则有可能不存在实数c∈(a,b)使得f(c)=0 | |
| D. | 若f(a)f(b)<0,则有且只有一个实数c∈(a,b)使得f(c)=0 |
1.下列函数中既是奇函数又是增函数的是( )
| A. | y=x3+x | B. | y=logax | C. | y=3x | D. | y=-$\frac{1}{x}$ |
8.若0<x<$\frac{1}{2}$,则x2(1-2x)有( )
| A. | 最小值$\frac{1}{27}$ | B. | 最大值$\frac{1}{27}$ | C. | 最小值$\frac{1}{3}$ | D. | 最大值$\frac{1}{3}$ |
