题目内容
(2012•宜宾一模)设数列{an}(n∈N)满足a0=0,a1=2,且对一切n∈N,有an+2=2an+1-an+2.
(I)求数列{an}的通项公式;
(II)当n∈N+时,令bn=
×
,Sn是数列{bn}的前n项和,求证:
≤Sn<
.
(I)求数列{an}的通项公式;
(II)当n∈N+时,令bn=
| n+1 |
| n+2 |
| 1 |
| an |
| 1 |
| 3 |
| 3 |
| 4 |
分析:(I)由an+2-an+1=an+1-an+2得,数列{an+1-an}为等差数列,且首项a1=2,公差为2,由此能求出数列{an}的通项公式;
(II)确定数列的通项,利用裂项法求和,借助于单调性,即可得到结论.
(II)确定数列的通项,利用裂项法求和,借助于单调性,即可得到结论.
解答:解:(I)由an+2-an+1=an+1-an+2可得:数列{an+1-an}为等差数列,且首项a1-a0=2-0=2,公差为2(3分)
∴an-an-1=(a1-a0)+2(n-1)=2+2(n-1)=2n(4分)
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+4+6+…+2n=
=n(n+1)(6分)
(II)由(I)可知:bn=
×
=-
=
(
-
)
∴Sn=b1+b2+…+bn=
[(1-
)+(
-
)+…+(
-
)]=
(1+
-
-
)<
(10分)
易知:Sn在n∈N*时,单调递增,
∴Sn≥S1=
(11分)
∴
≤Sn<
(12分)
∴an-an-1=(a1-a0)+2(n-1)=2+2(n-1)=2n(4分)
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+4+6+…+2n=
| n(2+2n) |
| 2 |
(II)由(I)可知:bn=
| n+1 |
| n+2 |
| 1 |
| an |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Sn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
易知:Sn在n∈N*时,单调递增,
∴Sn≥S1=
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 3 |
| 4 |
点评:本题考查数列递推式,考查叠加法的运用,考查数列求和,解题的关键是确定数列的通项,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
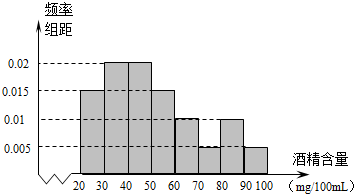 (2012•宜宾一模)《中华人民共和国道路交通安全法》
(2012•宜宾一模)《中华人民共和国道路交通安全法》